Mục lục
PHƯƠNG PHÁP GIẢI
Sử dụng linh hoạt các tỉ số liên quan tới trọng tâm của tam giác.
Ví dụ: Nếu $ \displaystyle \Delta $ABC có trung tuyến AM và trọng tâm G thì ta có
AG =$ \displaystyle \dfrac{2}{3}$ = AM , AG = 2GM; GM = $ \displaystyle \dfrac{1}{3}$AM; …
BÀI TẬP MINH HỌA
1A. Cho $ \displaystyle \Delta $ABC có hai đường trung tuyến BD, CE
a) Tính các tỉ số $ \displaystyle \dfrac{{BG}}{{BD}},\dfrac{{CG}}{{CE}}$
b) Chứng minh BD + CE > $ \displaystyle \dfrac{3}{2}$ BC
1B. Cho $ \displaystyle \Delta $ABC có BC = 8 cm, các đường trung tuyến BD, CE cắt nhau tại G. Chứng minh BD + CE > 12 cm.
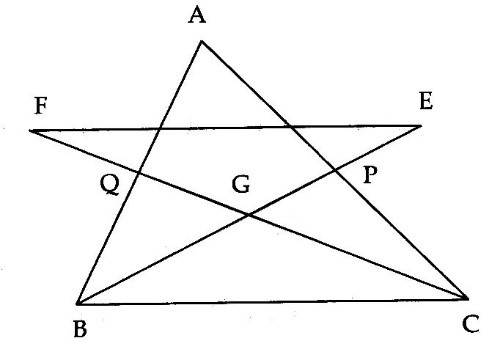
2A. Cho tam giác ABC có hai đường trung tuyến BP, CQ cắt nhau tại G. Trên tia đối của tia PB lấy điểm E sao cho PE = PG. Trên tia đối của tia QG lấy điểm F sao cho QF = QG. Chứng minh:
a) GB = GE, GC = GE; b) EF = BC và EF//BC.
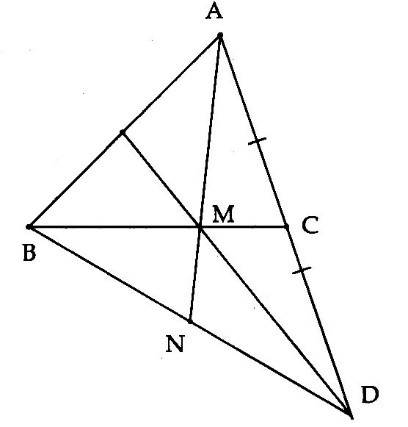
2B. Cho tam giác ABC có hai đường trung tuyến AD, BE cắt nhau tại G. Trên tia đối của tia DG lấy điểm M sao cho D là trung điểm của đoạn thẳng MG. Trên tia đối của tia EG lấy điểm N sao cho E là trung điểm GN. Chứng minh:
a) GN = GB, GM = GA; b) AN = MB và AN // MB.
HƯỚNG DẪN GIẢI
1A. Gọi giao điểm của hai đường trung tuyến BD,CE là G.
$ \displaystyle \Delta $GBC có: GB + GC > BC (bất đẳng thức tam giác).
Mà GB = $ \displaystyle \dfrac{2}{3}$BD, GC = $ \displaystyle \dfrac{2}{3}$CE nên: $ \displaystyle \dfrac{2}{3}$BD + $ \displaystyle \dfrac{2}{3}$CE > BC.
Do đó BD + CE > $ \displaystyle \dfrac{3}{2}$ BC.
1B. Tương tự 1A.
BD + CE > $ \displaystyle \dfrac{3}{2}$ . 8 = 12 cm.
2A. a) Vì G là trọng tâm $ \displaystyle \Delta $ABC nên BG = 2GP, CG = 2GQ.
Lại có PE = PG, QF = QG nên GE = 2GP, GF = 2GQ.
Do đó BG = GE,CG = GF.
b) Suy ra $ \displaystyle \Delta $GBC = $ \displaystyle \Delta $GEF (c.g.c)
Từ đó ta có EF = BC và $ \displaystyle \widehat{{GEF}}=\widehat{{GBC}}$
=> EF // BC.
2B. Tương tự 2A.
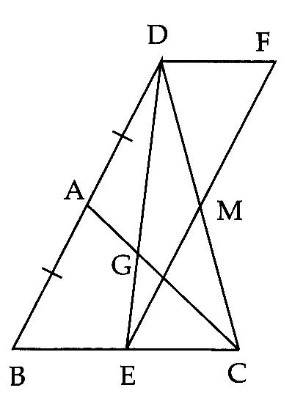
3A. a) Vì AD = AB nên A là trung điểm BD
=> CA là đường trung tuyến của $ \displaystyle \Delta $BCD
Mà AG = $ \displaystyle \dfrac{1}{3}$AC => G là trọng tâm $ \displaystyle \Delta $BCD
b) Ta có : BD || EF => $ \displaystyle \widehat{{BDE}}=\widehat{{DEF}}$ và DE || BC => $ \displaystyle \widehat{{BED}}=\widehat{{EDF}}$
=> $ \displaystyle \Delta $BED = $ \displaystyle \Delta $FDE (g.c. g) => BE = DF
(hai cạnh tương ứng) (1). Mặt khác do G là trọng tâm $ \displaystyle \Delta $BCD nên E là trung điểm BC
=> BE = EC (2).
Từ (1) và (2) suy ra EC = DF.
c) $ \displaystyle \Delta $DMF = $ \displaystyle \Delta $CME (g.c.g).
d) Do $ \displaystyle \Delta $DMF = $ \displaystyle \Delta $CME => MD = MC => M là trung điểm DC => BM là trung tuyến của $ \displaystyle \Delta $
=> G $ \displaystyle \in $BM => B, G, M thẳng hàng.
3B. Tương tự 3A.
a) M thuộc đường trung tuyến BC của $ \displaystyle \Delta $ABD mà BM = 2CM nên Mlà trọng tâm $ \displaystyle \Delta $ABD.
Do đó M thuộc trung tuyến AN.
=> Ba điểm A, M, N thẳng hàng.
b) DM là trung tuyến thứ ba của $ \displaystyle \Delta $ABD nên DM đi qua trung điểm của AB.