Cách so sánh hai cạnh trong một tam giác

PHƯƠNG PHÁP GIẢI

– Xét hai cạnh cần so sánh là hai cạnh của một tam giác.

– Tìm góc lớn hơn trong hai góc đối diện với hai cạnh ấy.

– Kết luận: Trong một tam giác cạnh đối diện với góc lớn hơn thì lớn hơn và ngược lại.

BÀI TẬP MINH HỌA

4A.    So sánh các cạnh của tam giác ABC, biết $ \displaystyle \widehat{A}$ = 80°, $ \displaystyle \widehat{B}$ = 40°.

4B.    So sánh các cạnh của tam giác PQR, biết $ \displaystyle \widehat{P}$ = 70°, $ \displaystyle \widehat{R}$ = 50°.

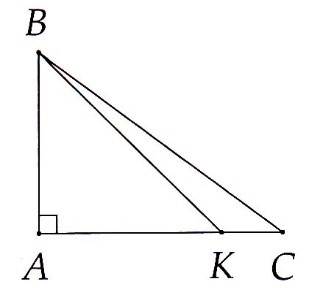
5A.    Cho tam giác ABC vuông tại A, điểm K nằm giữa A và C. So sánh độ dài BK và BC

5B.     Cho tam giác MNP vuông tại N. Trên tia đối của tia PN lấy điểm Q. So sánh độ dài MP và MQ.

6A.    Cho tam giác ABC có ba góc nhọn, AB < AC. Kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E. Gọi H là giao điểm cửa BD và CE. So sánh độ dài HB và HC.

6B.     Cho tam giác ABC có AB < AC. Tia phân giác của các góc B và C cắt nhau tại I. Từ I vẽ IH vuông góc với BC. So sánh độ dài HB và HC.

HƯỚNG DẪN GIẢI

4A.    Tính được $ \displaystyle \widehat{C}$ = 60°, do đó $ \displaystyle \widehat{B}<\widehat{C}<\widehat{A}$ => AC < AB < BC.

4B.     Tính được $ \displaystyle \widehat{Q}$ = 60°, do đó $ \displaystyle \widehat{R}<\widehat{Q}<\widehat{P}$ => PQ < PR < QR.

5A.    Chú ý $ \displaystyle \widehat{{BKC}}$ là góc ngoài của  $ \displaystyle \Delta $AKB

nên $ \displaystyle \widehat{{BKC}}$ >$ \displaystyle \widehat{A}$ = 90° > $ \displaystyle \widehat{C}$.

⇒ BK < BC

5B.     Tương tự 5A, ta có MP < MQ.

6A.    Áp dụng 3A, ta có $ \displaystyle \widehat{{HBC}}>\widehat{{HCB}}$=> HB < HC.

6B.     Dùng kết quả bài 3B, ta có $ \displaystyle \widehat{{IBC}}>\widehat{{ICB}}$ => IB < IC.

Mà HB² = IB² – IH², HC² = IC² –  IH². Suy ra HB < HC.