KIẾN THỨC CẦN NHỚ
1. Hình tam giác
a) Cấu trúc

b) Các loại hình tam giác
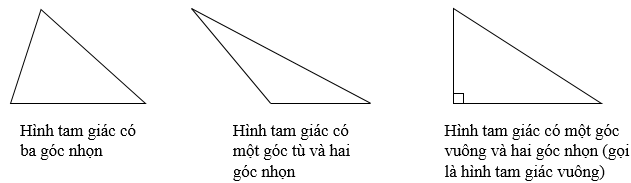
c) Cách xác định đáy và đường cao của hình tam giác
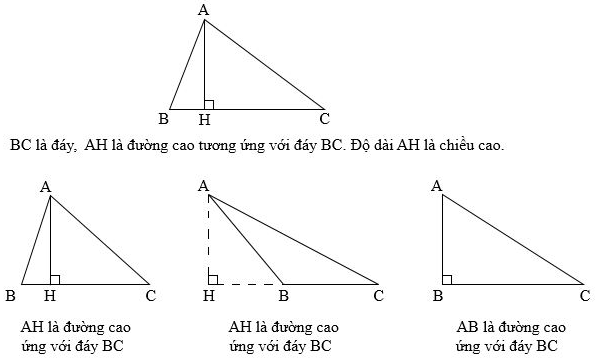
*Chú ý: Trong hình tam giác, độ dài đoạn thẳng từ đỉnh vuông góc với đáy tương ứng gọi là chiều cao của hình tam giác.
2. Diện tích hình tam giác
Quy tắc: Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.

*Chú ý: Muốn tính diện tích tam giác vuông ta lấy độ dài hai cạnh góc vuông nhân với nhau (cùng một đơn vị đo) rồi chia cho 2.
CÁC DẠNG TOÁN
Dạng 1: Tính diện tích tam giác khi biết độ dài đáy và chiều cao
Phương pháp: Áp dụng công thức: $\displaystyle S=\frac{a \times h}{2}$ hoặc $S=a \times h\colon 2$
( $S$ là diện tích, $a$ là độ dài đáy, $h$ là chiều cao)
Dạng 2: Tính độ dài đáy khi biết diện tích và chiều cao
Phương pháp: Từ công thức tính diện tích $\displaystyle S=\frac{a \times h}{2}$ hoặc $S=a \times h\colon 2$ ta có công thức tính độ dài đáy như sau: $\displaystyle a=\frac{S \times 2}{h}$ hoặc $a=S \times 2\colon h$
Dạng 3: Tính chiều cao khi biết diện tích và độ dài đáy
Phương pháp: Từ công thức tính diện tích $\displaystyle S=\frac{a \times h}{2}$ hoặc $S=a \times h\colon 2$ ta có công thức tính chiều cao như sau: $\displaystyle h=\frac{S \times 2}{a}$ hoặc $h=S \times 2\colon a$
Dạng 4: Toán có lời văn
Phương pháp: Đọc kĩ đề bài, xác định dạng toán trong bài rồi giải bài toán đó.
BÀI TẬP VÍ DỤ
Ví dụ 1: Tính diện tích hình tam giác có độ dài đáy là $10 \mathrm{~cm}$ và chiều cao là $6 \mathrm{~cm}$
Bài giải:
Diện tích hình tam giác đó là:
$10 \times 6\colon 2=30\left(\mathrm{~cm}^{2}\right)$
Đáp số: $30 \mathrm{~cm}^{2}$
Ví dụ 2: Tính diện tích hình tam giác có độ dài đáy là $5 \mathrm{~m}$ và chiều cao là $35 \mathrm{dm}$
Bài giải:
Đổi $5m=50 \mathrm{dm}$
Diện tích hình tam giác đó là:
$50 \times 35\colon 2=875\left(\mathrm{dm}^{2}\right)$
Đáp số: $875 {d}{m}^{2}$

