Cách tính số đo góc như thế nào ? Đây là điều mà các em học sinh lớp 7 phải làm được.
PHƯƠNG PHÁP
Sử dụng các tính chất:
– Hai góc đối đỉnh thì bằng nhau;
– Hai góc kề bù có tổng bằng 1800.
BÀI TẬP
Bài 1: Cho hình vẽ bên. Tính $ \displaystyle \widehat{{xOy^{\prime }}}$, biết $ \displaystyle \widehat{{xOy}}-\widehat{{yO{x}’}}=30{}^\circ $.
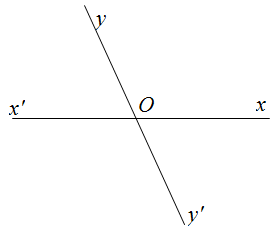
Bài 2: Cho hình vẽ bên. Biết $\widehat{A O C}+\widehat{B O D}=140^{\circ}$. Hãy tính số đo các góc $\widehat{A O C}, \widehat{C O B}, \widehat{B O D}, \widehat{D O A}$.
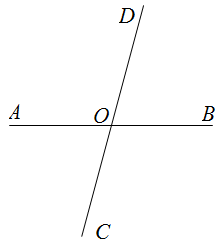
Bài 3: Cho góc $ \displaystyle \widehat{{xOy}}$ có số đo bằng 450. Vẽ hai tia $Om, On$ lần lượt là tia đối của tia $Oy, Ox$. Tính số đo các góc còn lại trên hình.
Bài 4: Vẽ hai đường thẳng cắt nhau sao cho trong các góc tạo thành có một góc bằng 1500. Tính số đo các góc còn lại.
Bài 5: Cho hai góc kề nhau $xOy$ và $yOz$ có tổng bằng 1500 và 900.
a) Tính số đo $xOy$ và $yOz$
b) Gọi $Oz’$ là tia đối của tia $Oz$. Hãy so sánh $xOz$ và $yOz’$.
Bài 6: Cho hai góc kề nhau $xOy$ và $yOz$ tổng bằng 1100 và $\widehat{x \widehat{O} y}-\widehat{y O} z=30^{\circ}$.
a) Tính số đo góc $xOy$ và $yOz$
b) Gọi $Oz’$ là tia đối của tia $Oz$. Hãy so sánh $xOz$ và $yOz’$.
Bài 7: Đường thẳng $xx’$ cắt đường thẳng $yy’$ tại O. Vẽ tia phân giác $Ot$ của $xOy$
a) Gọi $Ot’$ là tia đối của tia $Ot$. So sánh $xOt’$ và $t’Oy$.
b) Vẽ tia phân giác $Om$ của $xOy’$. Tính góc $mOt$.
Bài 8: Vẽ góc $x’Ay’$ đối đỉnh với góc $xAy$. Vẽ tia phân giác $Az$ của $ \displaystyle \widehat{{xAy}}$ và tia đối $At$ của tia $Az$. So sánh 2 góc $x’At$ và $y’At$.

