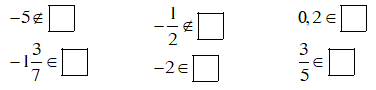PHƯƠNG PHÁP
Muốn xác định xem một số có phải số hữu tỉ không, ta hãy biến đổi xem số đó có dạng $ \dfrac{a}{b}$ với $ a,\,\,b\in \mathbb{Z}$; $ b\ne 0$ hay không.
BÀI TẬP
Bài toán 1: Các số 0,7; $ -1,2;$ $ 1\dfrac{3}{4};$ $ 2\dfrac{7}{8}$ có phải là số hữu tỉ không? Vì sao?
Bài toán 2: Các số $ -2,4;$ $ -1\dfrac{3}{4};$ $ -5$ có phải là các số hữu tỉ không? Vì sao?
Bài toán 3: Các số thập phân vô hạn tuần hoàn $ 0,\left( 3 \right);$ $ -1,2\left( {34} \right);$ $ -0,\left( 4 \right)$ có là các số hữu tỉ không? Vì sao?
Hướng dẫn:
- Nhận xét: $ 0,\left( 1 \right)=\dfrac{1}{9};$ $ 0,\left( {01} \right)=\dfrac{1}{{99}}$ nên $ 0,\left( 3 \right)=3.0,\left( 1 \right)=3.\dfrac{1}{9}=\dfrac{3}{9}$
- $ -1,2\left( {34} \right)=-\left( {1,2+0,0\left( {34} \right)} \right)$
$ \begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=-\left( {\dfrac{{12}}{{10}}+\dfrac{{34}}{{10}}.0,\left( {01} \right)} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=-\left( {\dfrac{{12}}{{10}}+\dfrac{{34}}{{10}}.\dfrac{1}{{99}}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=-\dfrac{{1222}}{{990}}=-\dfrac{{611}}{{495}}\end{array}$
Vậy $ 0,\left( 3 \right);$ $ -1,2\left( {34} \right);$ $ -0,\left( 4 \right)$ đều là số hữu tỉ.
Bài toán 4: Điền kí hiệu $ \left( {\in ,\,\,\notin ,\,\,\subset } \right)$ thích hợp vào ô vuông
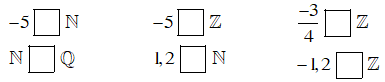
Bài toán 5: Điền tên các tập hợp $ \left( {\mathbb{N},\,\,\mathbb{Z},\,\,\mathbb{Q}} \right)$ vào ô vuông