MỤC LỤC
LÝ THUYẾT CẦN GHI NHỚ
Phương trình đường tròn
– Phương trình đường tròn có tâm $I (a;b)$, bán kính $R$ là $(x-2)^{2}+(y-b)^{2}=R^{2}$
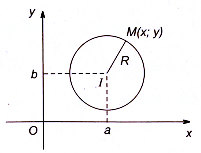
– Phương trình $x^{2}+y^{2}-2 a x-2 b y+c=0\left(a^{2}+b^{2}-c>0\right)$ là phương trình của đường tròn tâm $I (a;b)$ và bán kính $R=\sqrt{a^{2}+b^{2}-c}$.
Phương trình tiếp tuyến của đường tròn
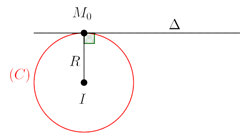
Cho trước điểm $M_{0}\left(x_{0} ; y_{0}\right)$ nằm trên đường tròn $(C)$ tâm $I$ có tọa độ $(a;b)$, tiếp tuyến tại $M_{0}$ của (C) có phương trình: $\left(x_{0}-a\right)\left(x-x_{0}\right)+\left(y_{0}-b\right)\left(y-y_{0}\right)=0$
CÁC DẠNG BÀI TẬP
Dạng 1: Nhận dạng phương trình đường tròn và tìm điều kiện để một phương trình là phương trình đường tròn

Dạng 2: Lập phương trình đường tròn đi qua các điểm

Dạng 3: Viết phương trình đường tròn tiếp xúc với đường thẳng

Dạng 4: Viết phương trình đường tròn nội tiếp tam giác

BÀI TẬP CÓ LỜI GIẢI
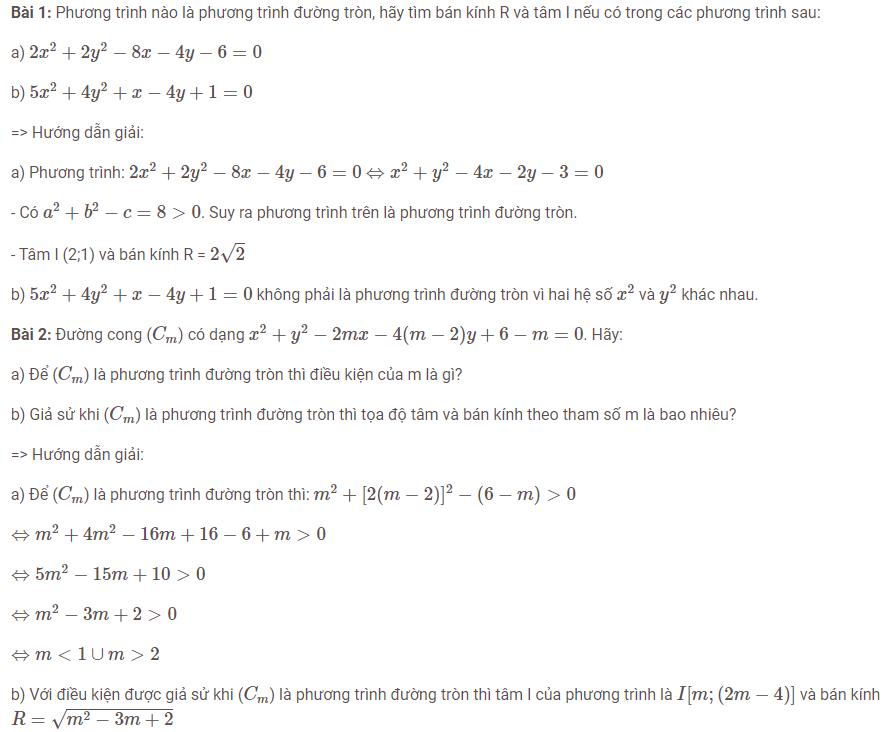

BÀI TẬP TỰ GIẢI


