Học Toán 123 chia sẻ cách giải phương trình bậc 2 và tính nhẩm nghiệm của phương trình bậc 2 trong một số trường hợp đặc biệt.
ĐỊNH NGHĨA PHƯƠNG TRÌNH BẬC 2
Phương trình bậc hai là phương trình có dạng: ax2 + bx + c = 0. Với
x là ẩn số
a, b, c là các số đã biết sao cho: a ≠ 0
a, b, c là những hệ số của phương trình và có thể phân biệt bằng cách gọi tương ứng với hệ số của x (theo phương trình trên thì a là hệ số bậc hai, b là hệ số bậc một, c là hằng số hay số hạng tự do).
CÁCH GIẢI PHƯƠNG TRÌNH BẬC 2
Giải phương trình bậc 2: ax2 + bx + c = 0 theo biệt thức delta (Δ)
Đặt $\Delta=b^{2}-4 a c$
– Nếu $\Delta<0$ thì phương trình vô nghiệm.
– Nếu $\Delta=0$ thì phương trình có nghiệm kép $x_{1}=x_{2}=-\dfrac{b}{2 a}$ Nếu $\Delta>0$ thì phương trình bậc 2 có hai nghiệm $x_{1}, x_{2}$
$
\begin{aligned}
&x_{1}=\dfrac{-b+\sqrt{\Delta}}{2 a}=\dfrac{-b+\sqrt{b^{2}-4 a c}}{2 a} \\
&x_{2}=\dfrac{-b-\sqrt{\Delta}}{2 a}=\dfrac{-b-\sqrt{b^{2}-4 a c}}{2 a}
\end{aligned}
$
ĐỊNH LÝ VI-ÉT VỚI PHƯƠNG TRÌNH BẬC 2
Công thức Vi-ét về quan hệ giữa các nghiệm của đa thức với các hệ số của nó. Trong trường hợp phương trình bậc hai một ẩn, được phát biểu như sau:
Nếu $x_{1}$ và $x_{2}$ là hai nghiệm của phương trình
$$
a x^{2}+b x+c=0(a \neq 0) \text { thì : }\left\{\begin{array}{c}
x_{1}+x_{2}=S=-\frac{b}{a} \\
x_{1} x_{2}=P=\frac{c}{a}
\end{array}\right.
$$
MỘT SỐ TRƯỜNG HỢP ĐẶC BIỆT CỦA PHƯƠNG TRÌNH BẬC 2
Nếu phương trình bậc 2 có:
- $\mathrm{a}+\mathrm{b}+\mathrm{c}=0$ (với $\mathrm{a}, \mathrm{b}, \mathrm{c}$ là các hệ số của phương trình bậc 2 , a khác 0 ) thì nghiệm của phương trình là: $x_{1}=1 ; x_{2}=\dfrac{c}{a}$
- $a-b+c=0$ (với $a, b, c$ là các hệ số của phương trình bậc 2 , a khác 0 ) thì nghiệm phương trình là: $x_{1}=-1 ; x_{2}=-\dfrac{c}{a}$
- Nếu $\mathrm{ac}<0(\mathrm{a}, \mathrm{c}$ trái dấu nhau) thì phương trình luôn có 2 nghiệm phân biệt.
CÁCH NHẨM NGHIỆM PHƯƠNG TRÌNH BẬC 2
Xuất phát từ định lý Vi-ét, chúng ta có các dạng toán tính nhẩm như sau:
Dạng 1: A = 1, B = Tổng, C = Tích
Nếu phương trình có dạng x2 – (u+v)x + uv = 0 thì phương trình đó có hai nhiệm u và v.
Nếu phương trình có dạng x2 + (u+v)x + uv = 0 thì phương trình có hai nghiệm -u và –v.
Tóm lại:
- x2 – (u+v)x + uv = 0 => x1 = u, x2 = v (1)
- x2 + (u+v)x + uv = 0 => x1 = -u, x2 = -v
Như vậy, với dạng này chúng ta cần thực hiện 2 phép nhẩm: “Phân tích hệ số c thành tích và b thành tổng”. Trong hai phép nhẩm đó, chúng ta nên nhẩm hệ số c trước rồi kết hợp với b để tìm ra hai số thỏa mãn tích bằng c và tổng bằng b.
Khi tiến hành, bạn nhẩm trong đầu như sau: Tích của hai nghiệm bằng c, mà tổng lại bằng b.
Ví dụ phương trình:
x2 – 5x + 6 = 0
Nhẩm: “Tích của hai nghiệm bằng 6, mà tổng lại bằng 5”. Hai số đó là: 2 và 3 vì 6 = 2×3 và 5 = 2 + 3. Vậy phương trình có hai nghiệm x = 2, x = 3.
x2 – 7x + 10 = 0
Nhẩm: “Tích của hai nghiệm bằng 10, mà tổng lại bằng 7”. Hai số đó là: 2 và 5 vì 10 = 2×5 và 7 = 2 + 5. Vậy phương trình có hai nghiệm x = 2, x = 5.
Dạng 2: A + B + C = 0 và A – B + C = 0
x2 – (u+v)x + uv = 0 => x1 = u, x2 = v (1)
- Nếu thay v = 1 vào (1) thì chúng ta sẽ có trường hợp nhẩm nghiệm quen thuộc a + b + c = 0, với a = 1, b = -(u+1), c = u.
- Nếu thay v = -1 vào (1) thì bạn sẽ có trường hợp nhẩm nghiệm a – b + c = 0, với a = 1, b = -(u-1), c = -u.
Do loại này đã quá quen thuộc và thường gặp, nên bài viết không xét các ví dụ cho trường hợp này mà tập trung vào Dạng 1 và Dạng 3.
Dạng 3: Hai nghiệm là nghịch đảo của nhau
Nếu u ≠ 0 và v = 1/u thì phương trình (1) có dạng:
$x^{2}-\left(u+\dfrac{1}{u}\right) x+u \cdot \dfrac{1}{u}=0 \Leftrightarrow u . x^{2}-\left(u^{2}+1\right) x+u=0$
Khi đó: Phương trình có hai nghiệm là nghịch đảo của nhau x= u, x = 1/u. Đây cũng là trường hợp hay gặp khi giải toán. Ví dụ phương trình:
- 2x2 – 5x + 2 = 0 có hai nghiệm x = 2, x = 1/2
- 3x2 – 10x + 3 = 0 có hai nghiệm x = 3, x = 1/3
Ví dụ nhẩm nghiệm của PT bậc 2

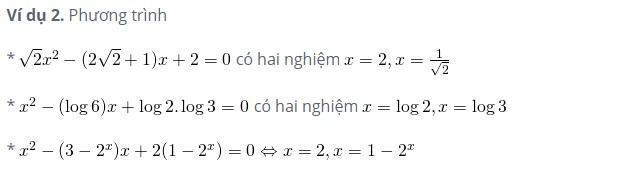
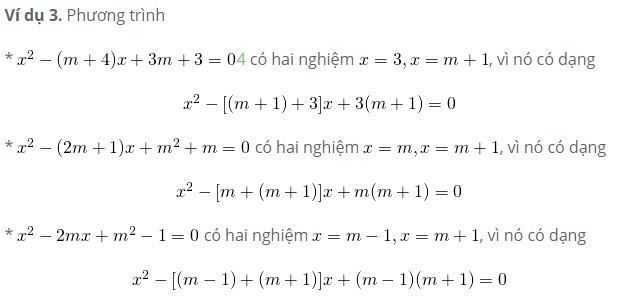
BÀI TẬP GIẢI PHƯƠNG TRÌNH BẬC 2
a) 2x2 + 6x + 5 = 0
b) x2 – 4x + 4 = 0
c) 2x2 + 7x – 3 = 0.

