Mục lục
PHƯƠNG PHÁP
Cách giải phương trình bậc hai bằng đồ thị
Để giải phương trình bậc hai $a x^{2}+{bx}+{c}=0$ (tức là $a x^{2}=-{bx}-{c}$ ) bằng đồ thị, ta vẽ parabol $y=a x^{2}$ và đường thẳng $y={bx}-{c}$ trong cùng một hệ trục toạ độ, rồi xác định hoành độ các giao điểm của chúng (nếu có).
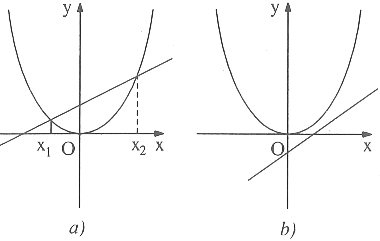
- Nếu đường thẳng cắt parabol tại hai điểm (Hình a) thì phương trình có hai nghiệm (trường hợp này ứng với $\Delta>0$ ).
- Nếu đường thẳng không giao với parabol (Hình b) thì phương trình vô nghiệm (trường hợp này ứng với $\Delta<0$ ).
- Nếu đường thẳng tiếp xúc với parabol (Hình c) thì phương trình có nghiệm kép (trường hợp này ứng với $\Delta=0$ ).
*Chú ý:
Một đường thẳng gọi là tiếp xúc với parabol nếu nó có một điểm chung duy nhất với parabol và parabol nằm về một phía của đường thẳng (Hình c). Ở Hình d, đường thẳng $x = m$ cũng chỉ có một điểm chung với parabol nhưng ta không gọi là tiếp xúc với parabol.
Vị trí tương đối giữa parabol $y=a x^{2}(a \neq 0)$ và đường thẳng $y={mx}+n$
Xét phương trình: $ a x^{2}=m x+n $ tức là $a x-m x-n=0 $
- Đường thẳng cắt parabol tại hai điểm phân biệt ⇔ (1) có $\Delta>0$.
- Đường thẳng không giao với parabol ⇔ (1) có $\Delta<0$.
- Đường thẳng tiếp xúc với parabol ⇔ (1) có $\Delta=0$.
VÍ DỤ CÓ LỜI GIẢI
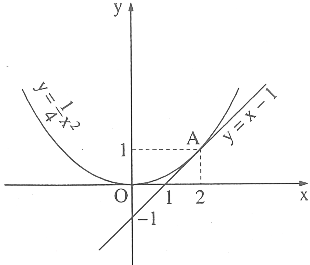
Ví dụ 1: Cho parabol $y=a x^{2}$ tiếp xúc với đường thẳng $y=x-1$,
a) Xác định hệ số $a$;
b) Tìm toạ độ tiếp điểm của đường thẳng và parabol;
c) Vẽ parabol và đường thẳng nói trên cùng một hệ trục toạ độ.
Giải
a) Điều kiện để parabol $y=a x^{2}$ tiếp xúc với đường thẳng $y=x-1$ là phương trình $a x^{2}=x-1$ có nghiệm kép.
$a \neq 0 \text { và } \Delta=0 \Leftrightarrow a \neq 0 \text { và } 1-4 a=0 \Leftrightarrow a=\dfrac{1}{4} \text {. }$
b) Hoành độ của tiếp điểm là nghiệm của phương trình
$\dfrac{1}{4} x^{2}-x+1=0$
Giải phương trình trên ta có
$\begin{aligned} x^{2}-4 x+4=& 0 \Leftrightarrow(x-2)^{2}=0 \\ & \Leftrightarrow x=2 . \end{aligned}$
Với $x=2$ thì $y=\dfrac{1}{4} \cdot 2^{2}=1 .$
Tọa độ của tiếp điểm $a$ là $(2 ; 1)$.
c) Xem hình vẽ.
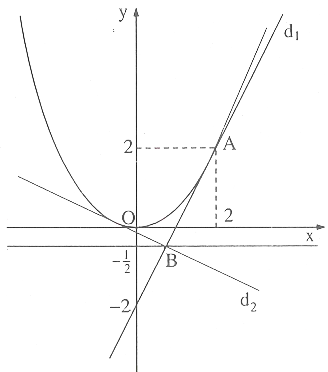
Ví dụ 2: Cho parabol $y=\dfrac{1}{2} x^{2}$
a) Chứng minh rằng đường thẳng $y=2 x-2\left(d_{1}\right)$ tiếp xúc với parabol. Tìm toạ độ của tiếp điểm.
b) Cho biết điều kiện để hai đường thẳng $y=a x+b$ và $y=a^{\prime} x+b^{\prime}$ vuông góc với nhau là aa’ $=-1$. Xác định tiếp tuyến $d_{2}$ của parabol sao cho $d_{1} \perp d_{2}$.
c) Tim toạ độ giao điểm của hai đường thẳng $d_{1}$ và $d_{2}$.
d) Chứng minh rằng giao điểm các tiếp tuyến của parabol mà vuông góc với nhau nằm trên đường thẳng $y=\dfrac{1}{2}$.
Giải



BÀI TẬP ÁP DỤNG
Bài 1: Cho parabol $y=x^{2}$. Xác định hệ số $n$ để đường thẳng $y=2 x+n$ tiếp xúc với parabol. Tìm toạ độ của tiếp điểm.
Bài 2: Cho parabol $y=\dfrac{1}{2} x^{2}$ và đường thẳng $y={mx}+n$.
Xác định các hệ số ${m}$ và $n$ để đường thẳng đi qua điểm $a(-1 ; 0)$ và tiếp xúc với parabol. Tìm toạ độ của tiếp điểm.
Bài 3: Cho parabol $y=\dfrac{x^{2}}{4}$. Lập phương trình đường thẳng đi qua điểm $A(-1 ;-2)$ và tiếp xúc với parabol. Tìm toạ độ của tiếp điểm.
Bài 4: Cho parabol $y=x^{2}$ và đường thẳng $y=x+n$.
a) Với giá trị nào của $n$ thì đường thẳng cắt parabol tại hai điểm phân biệt?
b) Xác định toạ độ giao điểm của parabol và đường thẳng nếu $n=2$.
Bài 5: Vẽ đồ thị của hàm số $y=x^{2}+1+\left|x^{2}-1\right|$.
Bài 6: Giải các phương trình sau bằng phương pháp đồ thị :
a) $2 x^{2}-1=|x-2|$;
b) $x^{2}-4|x-1|+4=0$
