Cách giải hệ phương trình có chứa tham số dành cho học sinh lớp 9 qua phương pháp giải và các bài tập minh họa dễ hiểu nhất.
Từ đó giúp học sinh không còn thấy khó khăn với dạng toán này nữa.
I. Lý thuyết, cách giải chung
Cho hệ phương trình $\left\{\begin{array}{l}a x+b y=c \\ a^{\prime} x+b^{\prime} y=c\end{array},\left(^{*}\right)\right.$
– Để giải hệ phương trình (*) ta thường dùng phương pháp thế hoặc cộng đại số.
– Từ hai phương trình của hệ phương trình (*), sau khi dùng phương pháp thế hoặc phương pháp cộng đại số, ta thu được một phương trình mới gồm một ẩn. Khi đó số nghiệm của phương trình mới bằng số nghiệm hệ phương trình đã cho.
*Chú ý: Với trường hợp $a^{\prime} ; b^{\prime} ; c^{\prime} \neq 0$
– Hệ phương trình có nghiệm duy nhất $\Leftrightarrow \frac{a}{a^{\prime}} \neq \frac{b}{b^{\prime}}$;
– Hệ phương trình vô nghiệm $\Leftrightarrow \frac{a}{a^{\prime}}=\frac{b}{b^{\prime}} \neq \frac{c}{c^{\prime}}$;
– Hệ phương trình vô số nghiệm $\Leftrightarrow \frac{a}{a^{\prime}}=\frac{b}{b^{2}}=\frac{c}{c^{\prime}}$.
II. Các dạng bài tập
Dạng 1: Giải và biện luận hệ phương trình
Phương pháp giải: Để giải và biện luận hệ phương trình (*) ta làm như sau:
– Bước 1: Sử dụng các phương pháp giải hệ phương trình cơ bản đã học như thế, cộng đại số, ta thu được phương trình mới (chỉ còn một ẩn).
– Bước 2: Giải và biện luận phương trình mới, từ đó đi đến kết luận về giải và biện luận hệ phương trình đã cho.
*Chú ý: Số nghiệm của hệ phương trình (*) bằng số nghiệm của phương trình mới.

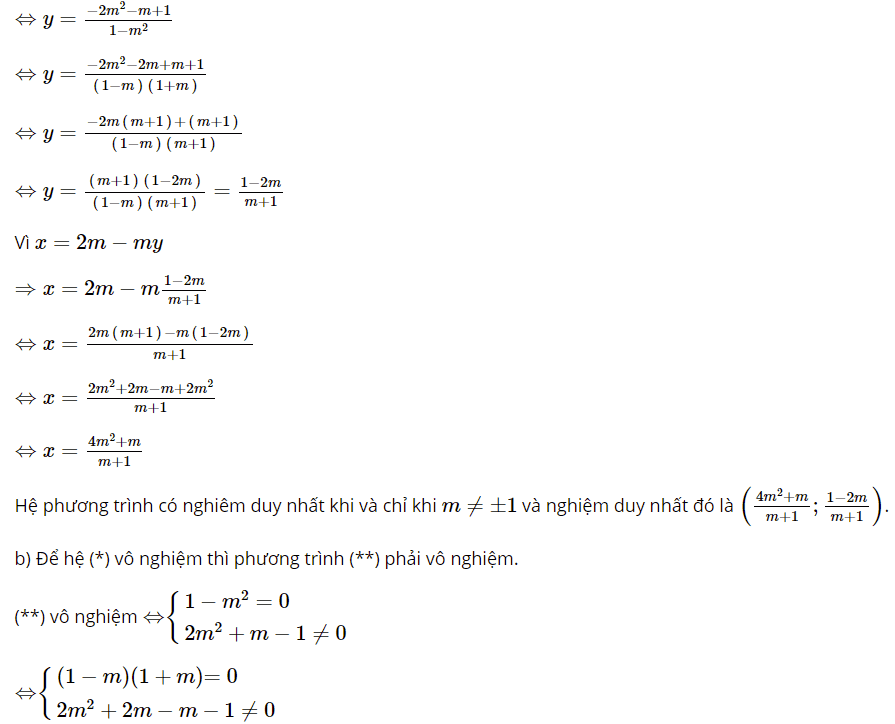


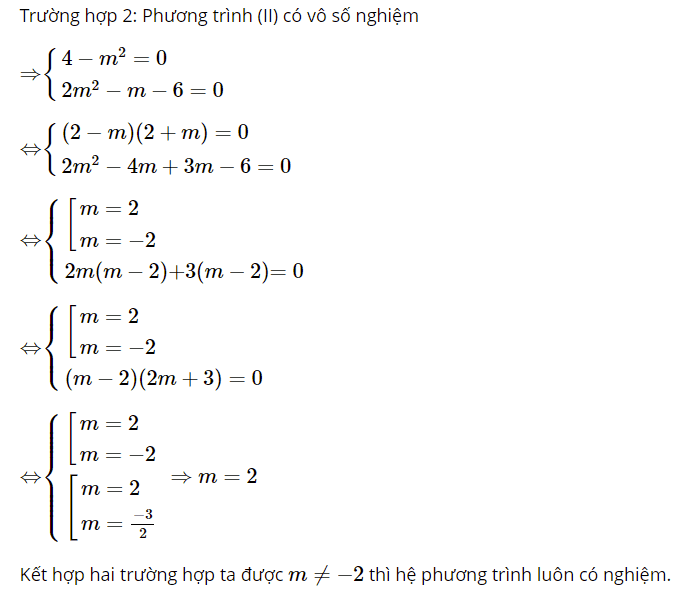
Dạng 2: Tìm điều kiện của m để hệ phương trình thỏa mãn điều kiện cho trước.
Phương pháp giải:
– Bước 1: Đặt điều kiện để hệ phương trình có nghĩa (nếu có).
– Bước 2: Tìm điều kiện để hệ phương trình có nghiệm duy nhất.
– Bước 3: Giải hệ phương trình tìm nghiệm (x; y) theo tham số m.
– Bước 4: Thay x; y vào điều kiện đề bài và giải điều kiện.
– Bước 5: Kết luận.

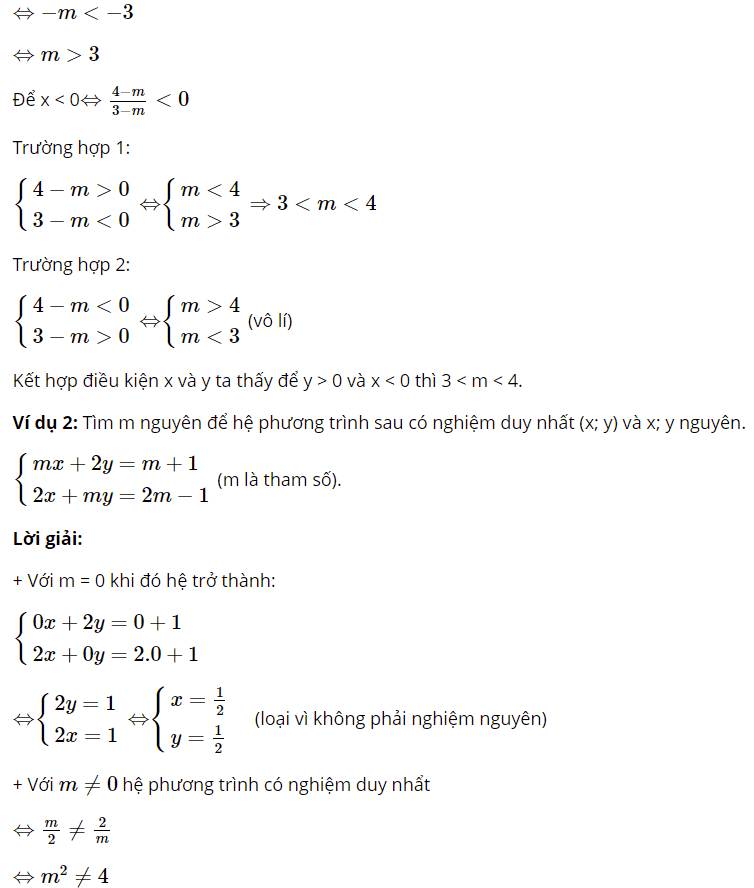
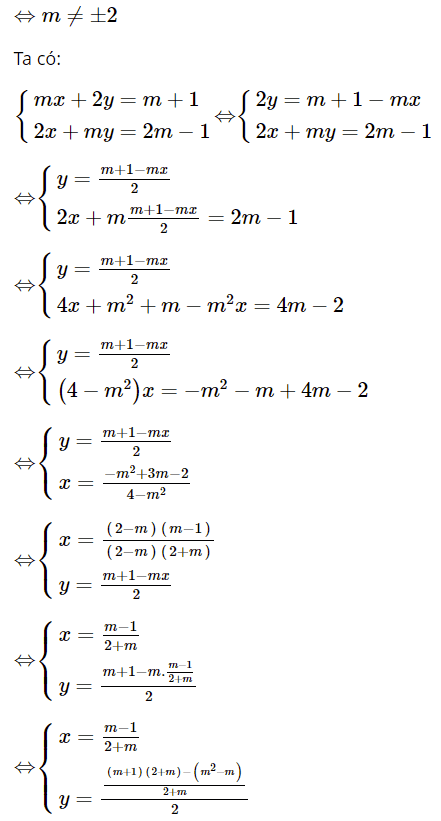
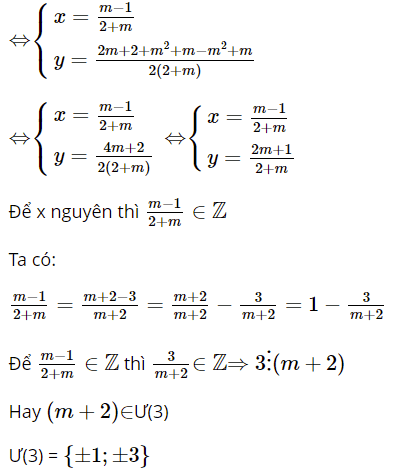


Dạng 3: Tìm hệ thức liên hệ giữa các ẩn trong hệ phương trình không phụ thuộc vào tham số m
Phương pháp giải: Ta thực hiện theo ba bước
– Bước 1: Tìm điều kiện của tham số m để hệ phương trình có nghiệm duy nhất.
– Bước 2: Dùng phương pháp cộng đại số hoặc thế làm mất tham số m.
– Bước 3: Kết luận


III. Bài tập vận dụng



