Đề thi HSG Toán 9 quận Ba Đình 2022-2023

Đề thi Toán lớp 9
Comments
Đây là bài thứ 109 of 181 trong series Đề thi HSG Toán 9

Đề thi HSG Toán 9

Đề thi chọn học sinh giỏi môn Toán lớp 9 quận Ba Đình, thành phố Hà Nội, năm học 2022-2023. Thời gian làm bài 150 phút.

Ngày thi 29 tháng 11 năm 2022. Hình thức thi tự luận gồm 5 bài.

Đề thi HSG Toán 9 quận Ba Đình 2022-2023

Đáp án Đề thi HSG Toán 9 quận Ba Đình năm 2022-2023

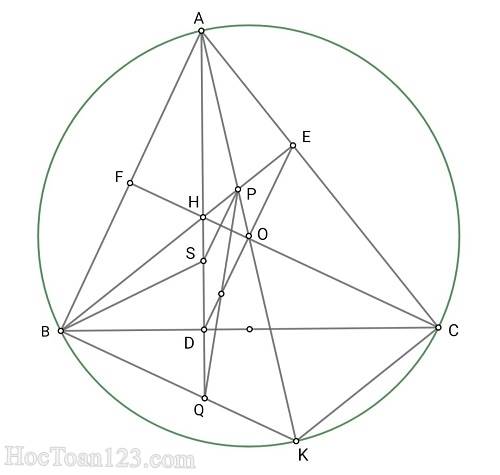
Đề thi HSG Toán 9 quận Ba Đình 2022-2023

Đề thi HSG Toán 9 quận Ba Đình 2022-2023
Bài IV: Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Các đường cao AD, BE, CF đồng quy tại H. Gọi M là trung điểm của BC. Kẻ đường kính AK của đường tròn (O).
1. Chứng minh: H, M, K thẳng hàng
2. Gọi P là giao điểm của AK với BE, Q là giao điểm của AD với BK. Chứng minh: góc BAD = CAK và ∆AEP ~ ∆BDQ
3. Chứng minh: DE chia đều PQ
Lời giải:
b. ∆AOC cân => góc CAK = 90° – AOC/2 = 90° – ABD = BAD
Xét ∆AEP và ∆BDQ, có:
Góc AEP = BDQ = 90°
Góc PAE = BAD (cmt) = QBD (góc tạo bởi các cạnh tương ứng vuông góc)
=> ∆AEP ~ ∆BDQ (g.g)
c. => Góc APE = BQD = BSD (với S là điểm đối xứng với Q qua D)
=> Góc APB = ASB
=> Tứ giác APSB nội tiếp
=> Góc ASP = ABE = ECH = EDH
=> SP // DE, vì DS = DQ nên DE đi qua trung điểm của PQ (đpcm)
Đề thi HSG Toán 9 quận Ba Đình 2022-2023
Series Navigation<< Đề thi HSG Toán 9 vòng 2 huyện Diễn Châu, Nghệ An 2022-2023Đề thi HSG Toán 9 huyện Sơn Hòa, Phú Yên 2022-2023 >>

Trả lời

Email của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu *