PHƯƠNG PHÁP GIẢI
Vận dụng Định lý 2.
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Trong tam giác ABC, nếu $ \displaystyle \widehat{B}>\widehat{C}$thì AC > AB.
BÀI TẬP MINH HỌA
1A. Cho tam giác ABC có AB <AC. Kẻ AH vuông góc với BC tại H. So sánh độ dài HB và HC
1B. Cho tam giác MNP có MN = 3 cm, MP = 4 cm. Kẻ MK vuông góc với NP tại K. So sánh độ dài KN và KP.
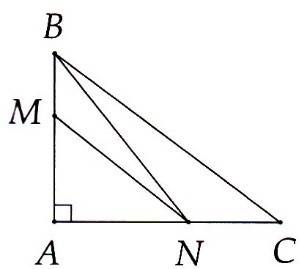
2A. Cho tam giác ABC vuông tại A. Trên các cạnh AB, AC lần lượt lấy các điểm M, N.
a) Chứng minh MN < BN < BC.
b) Có thể nói BN có hình chiếu xuống AC là AN còn CM có hình chiếu xuống AC là AC nên CM > BN được không?
2B. Cho tam giác ABC vuông tại A. Trên cạnh AC lấy các điểm M, N (M nằm giữa A, N). So sánh các độ dài BM, BN, BC.
3A. Cho tam giác ABC có AB > AC. Kẻ AH vuông góc với BC tại H, điểm D thuộc đoạn AH. So sánh:
a) DB và DC; b) DB và AB.
3B. Cho tam giác MNP có MN < MP. Kẻ MK vuông góc với NP tại K. Trên tia đối của tia MK lấy điểm Q. So sánh độ dài QN và QP.
HƯỚNG DẪN GIẢI
1A. Đường xiên AB < AC nên hình chiến HB < HC.
1B. Đường xiên MN < MP nên hình chiếu KN < KP.
2A. Hình chiếu AM < AB nên đường xiên MN < BN. Hình chiếu AN < AC nên đường xiên BN < BC. Bởi vậy MN < BN < BC.
b) Không được vì M và B khác nhau.
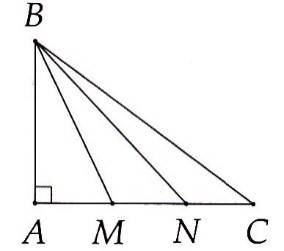
2B. Tương tự 2A, chú ý: AM < AN < AC.
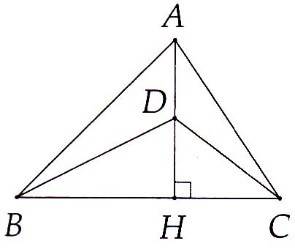
3A. a) Đường xiên AB > AC nên hình chiếu HB > HC. Hình chiếu HB > HC nên đường xiên DB > DC.
b) BA và BD có hình chiếu lần lượt là AH và DH. Mà AH > BH => BA > BD.
3B. Tương tự 3A, chú ý KN < KP.

