LÝ THUYẾT CẦN GHI NHỚ
Để chứng minh 3 điểm thẳng hàng ở lớp 7 chúng ta thường áp dụng những cách sau:
– Nếu 3 điểm cùng tạo với nhau thành 1 góc bằng 180° thì 3 điểm đó thẳng hàng (đã học ở lớp 6).
– Qua một điểm chỉ kẻ được duy nhất một đường thẳng song song (hoặc vuông góc) với đường thẳng cho trước (tiên đề Ơ clit).
– Chứng minh 3 điểm cùng nằm trên một đường thẳng (đường cao, đường trung tuyến, đường phân giác).
BÀI TẬP ÁP DỤNG
Dưới đây là các ví dụ chứng minh 3 điểm thẳng hàng có lời giải để các em học và áp dụng.
Ví dụ 1: Cho ΔABC vuông tại B. Trên nữa mặt phẳng bờ BC không có điểm A, vẽ tia Cx vuông góc BC. Trên tia Cx lấy M sao cho CM = AB. Chứng minh A, M và D là trung điểm của BC thẳng hàng.
Giải
Xét ΔABD và ΔMCD, ta có: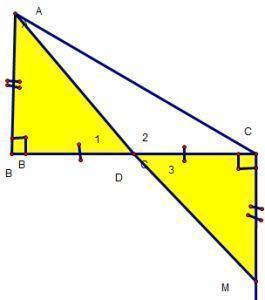
$\widehat{B}=\widehat{C}=90^{\circ}$
AB = CM (gt)
DB = DC (D là trung điểm của BC)
⇒ ΔABD = ΔMCD (2 cạnh góc vuông)
⇒ $\widehat{D_{1}}=\widehat{D_{3}}$
Mặt khác: $\widehat{D_{1}}+\widehat{D_{2}}=180^{\circ}$ (B, D, C thẳng hàng)
⇒ $\widehat{D_{2}}+\widehat{D_{3}}=180^{\circ}$
Hay: $\widehat{A D M}=180^{\circ}$
⇒ A, D, M thẳng hàng ( góc bẹt)
Nhận xét: Ở bài này chứng minh 3 điểm thẳng hàng bằng cách chứng minh cho góc tạo bởi 3 điểm bằng 180°.
Ví dụ 2: Cho tam giác ABC . gọi D, E lần lượt là trung điểm của AB, AC. Trên tia đối của tia DC, lấy điểm M sao cho MD = CD. Trên tia đối của tia EB, lấy điểm N sao cho EN = BE. Chứng minh: A là trung điểm của MN.
Giải
Xét ΔBCD và ΔBMD, ta có: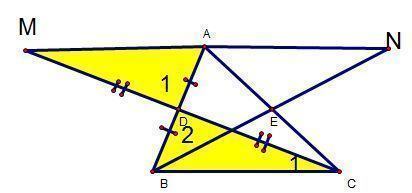
DB = DA (D là trung điểm của AB)
$\widehat{D_{1}}=\widehat{D_{2}}$ (đối đỉnh).
DC = DM (gt).
⇒ ΔBCD = ΔBMD (c -g -c)
⇒ $\widehat{C_{1}}=\widehat{M}$ và BC = AM.
Mà: $\widehat{C_{1}}; \widehat{M}$ ở vị trí so le trong. => BC // AM.
Chứng minh tương tự, ta được: BC // AN và BC = AN.
Ta có: BC // AM (cmt) và BC // AN (cmt)
⇒ A, M, N thẳng hàng. (1)
BC = AM và BC = AN => AM = AN (2).
Từ (1) và (2), suy ra: A là trung điểm của MN.
Nhận xét: Chứng minh 3 điểm A, M, N thẳng hàng trước, sau đó chứng minh AM = AN
Ví dụ 3:
Cho tam giác ABC vuông góc tại A có góc B = 53°.
a) Tính góc C.
b) Trên cạnh BC, lấy điểm D sao cho BD = BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. Chứng minh rằng: ΔBEA = ΔBED.
c) Qua C, vẽ đường thẳng vuông góc với BE tại H. CH cắt đường thẳng AB tại F. Chứng minh: ΔBHF = ΔBHC.
d) Chứng minh rằng: ΔBAC = ΔBDF và 3 điểm D, E, F thẳng hàng.
Giải
a. Tính góc C
Xét ΔBAC, ta có:
$\widehat{A}+\widehat{B}+\widehat{C}=180^{\circ}$
⇒ $\widehat{C}=180^{0}-(\widehat{A}+\widehat{B})$
⇒ $\widehat{C}=180^{0}-\left(90^{0}+53^{0}\right)=37^{0}$
b. ΔBEA = ΔBED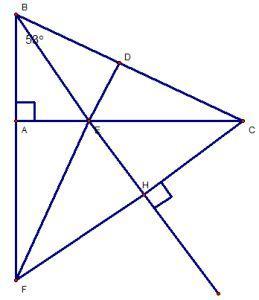
Xét ΔBEA và ΔBED, ta có:
BE cạnh chung.
$\widehat{A B E}=\widehat{D B E}$ (BE là tia phân giác của góc B)
BD = BA (gt)
⇒ ΔBEA = ΔBED (c – g – c)
c. ΔBHF = ΔBHC
Xét ΔBHF và ΔBHC, ta có:
BH cạnh chung.
$\widehat{A B H}=\widehat{D B H}$ (BE là tia phân giác của góc B)
$\widehat{B H F}=\widehat{B H C}=90^{\circ}$ (gt)
⇒ ΔBHF = ΔBHC (cạnh huyền – góc nhọn)
⇒ BF = BC (cạnh tương ứng)
d. ΔBAC = ΔBDF và D, E, F thẳng hàng
Xét ΔBAC và ΔBDF, ta có:
BC = BF (cmt)
Góc B chung.
BA = BC (gt)
⇒ ΔBAC = ΔBDF
⇒ $\widehat{B A C}=\widehat{B D F}$
Mà: $\widehat{B A C}=90^{\circ}$ (gt)
Nên: $\widehat{B D F}=90^{\circ}$ hay BD ⊥ DF (1)
Mặt khác: $\widehat{B A E}=\widehat{B D F}$ (hai góc tương ứng của ΔBEA = ΔBED)
Mà: $\widehat{B A E}=90^{\circ}$ (gt)
Nên: $\widehat{B D E}=90^{\circ}$ hay BD ⊥ DE (2)
Từ (1) và (2), suy ra: DE trùng với DF
Hay 3 điểm D, E, F thẳng hàng.
BÀI TẬP TỰ GIẢI
Bài 1: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm F sao cho AB = FA. Trên tia đối của tia AC lấy điểm E sao cho AC = AE.
a) Chứng minh: ΔEAF = ΔCAB
b) Gọi K là trung điểm EF và D là trung điểm BC. Chứng minh: KB = FD.
d) Chứng minh: K, A, D thẳng hàng.
Bài 2: Cho Δ ABC có M là trung điểm của AB. Trên tia đối của tia MC lấy điểm D sao cho MD = MC.
a) Chứng minh ΔMAD = ΔMBC và AD // CB.
b) Lấy N thuộc AD; NM cắt BC tại P. Chứng minh AN = BP.
c) Trên nửa mặt phẳng bờ AB không chứa điểm D, vẽ tia AE sao cho góc EAB + góc ABC = 180°.
Chứng minh D, A, E thẳng hàng.


vd 3. câu c sai trường hợp bằng nhau cuatr tam giác r. pk là cgv-gnk mới đúng