PHƯƠNG PHÁP GIẢI
Thay tọa độ điểm M (x0;y0) vào y = ax.
Từ đó xác định được a
BÀI TẬP MINH HỌA
5A. Xác định hệ số a của hàm số y = ax, biết đổ thị hàm số đi qua điểm:
a) A (1 ; -2); b) B (-3; 4).
5B. Xác định hệ số a của hàm số y= (a- 1) x, biết đồ thị hàm số đi qua điểm:
a) A ( 1; 2);
b) B (2; -6).
6A. Cho hàm số y = (2a +l.)x. Hãy xác định hệ số a biết:
a) Đồ thị của hàm số đi qua điểm A (-1; 3);
b) Đồ thị của hàm số đi qua điểm B (2;0);
c) Đồ thị của hàm số là đường phân giác góc phần tư thứ I, III
6B. Cho hàm số y = (3a – l)x. Hãy xác định hệ số a biết:
a) Đồ thị của hàm số đi qua điểm A (-2; -4);
b) Đồ thị của hàm số đi qua điểm B (1; 0);
c) Đồ thị của hàm số là đường phân giác góc phần tư thứ II; IV.
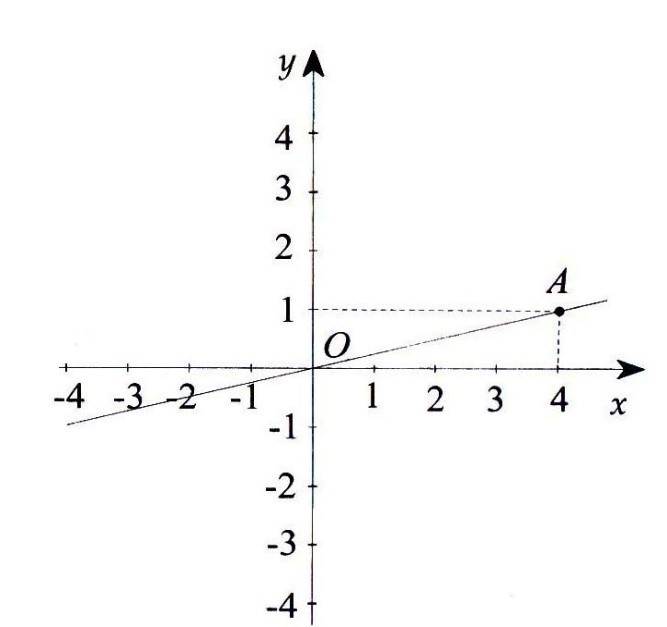
7A. Cho đường thẳng OA trong hình vẽ là đồ thị của hàm số y = ax.
a) Hãy xác định hệ số a?
b) Đánh dấu điểm trên đồ thị có hoành độ bằng 2?
c) Đánh dấu điểm trên đồ thị có tung độ bằng 1?
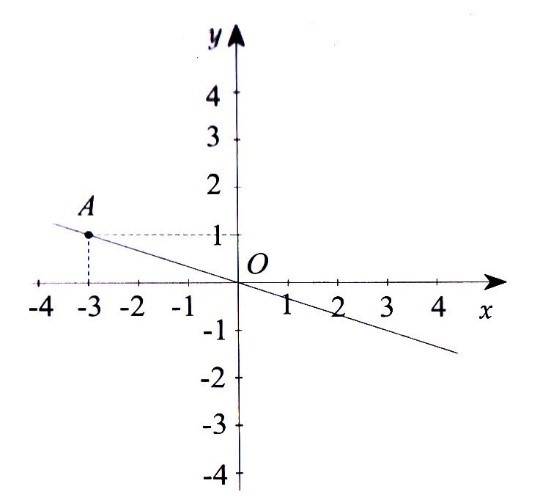
7B. Cho đường thẳng OA trong hình vẽ là đồ thị của hàm số y = ax.
a) Hãy xác định hệ số a?
b) Đánh dấu điểm trên đồ thị có hoành độ bằng 3?
c) Đánh dấu điểm trên đồ thị có tung độ bằng – $ \displaystyle \dfrac{3}{2}$?
HƯỚNG DẪN GIẢI
5A. a) Điểm A (1;-2) thuộc đồ thị của hàm số y = ax nên thay x = 1;y = -2 ta có -2 = a.1. Tìm a= -2
b) Điểm B(-3;4) thuộc đồ thị của hàm số y = ax nên thay x = -3;y = 4 ta có 4 = a.(-3). Tìm được a = $ \displaystyle \dfrac{4}{3}$
5B. Tương tự 5A. a) a = 3. b) a = -2.
6A. Tương tự 5A. a) a = -2. b) a = -$ \displaystyle \dfrac{1}{2}$ c) a = 0
6B. Tương tự 5A. a) b) HS tự làm
c) Vì đồ thị là đường phân giác của góc phần tư thứ II; IV nên có dạng y
7A. a) Đồ thị của hàm số y = ax đi qua điểm A (4;1) nên ta có:
1= a .4 => a =$ \displaystyle \dfrac{1}{4}$
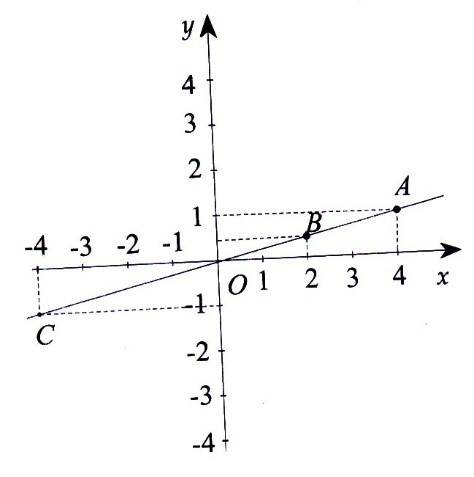
b) Từ điểm trên 2 trục hoành ta kẻ đường thẳng song song với trục tung cắt OA tại B. Ta được điểm B có hoành độ bằng 2.
c) Từ điểm trên -1 trục tung ta kẻ đường thẳng song song với trục hoành, cắt OA tại C. Ta được điểm C có tung độ bằng -1
7B. Tương tự 7A.

