Khảo sát và vẽ đồ thị hàm số bậc hai $y=ax^{2}$

Hướng dẫn học sinh lớp 9 khảo sát và vẽ đồ thị hàm số bậc hai y = ax^2 qua lý thuyết và ví dụ minh họa dễ hiểu, nhìn là làm được ngay.

Các em cần nắm vững lý thuyết và quan sát ví dụ sau đó tự làm bài tập.

Khảo sát sự biến thiên của hàm số $y=ax^{2}$ (a≠0)

Tập xác định: $ D=\mathbb{R}$

– Nếu a > 0, hàm số đồng biến khi $ x>0$, hàm số nghịch biến khi $ x<0$

– Nếu a < 0, hàm số đồng biến khi $ x<0$, hàm số nghịch biến khi $ x>0$

Cách vẽ đồ thị hàm số $y=ax^{2}$

Các bước thực hiện như sau:

– Bước 1: Lập bảng giá trị $ \displaystyle (x;y)$ tương ứng.

– Bước 2: Tiến hành vẽ đồ thị hàm số đi qua các điểm từ bảng giá trị.

*Chú ý: Đồ thị hàm số $ y=ax^{2}$ là đường cong Parabol đi qua gốc tọa độ $ O$ và nhận $ Oy$ làm trục đối xứng.

Bài tập khảo sát và vẽ đồ thị hàm số y = ax^2

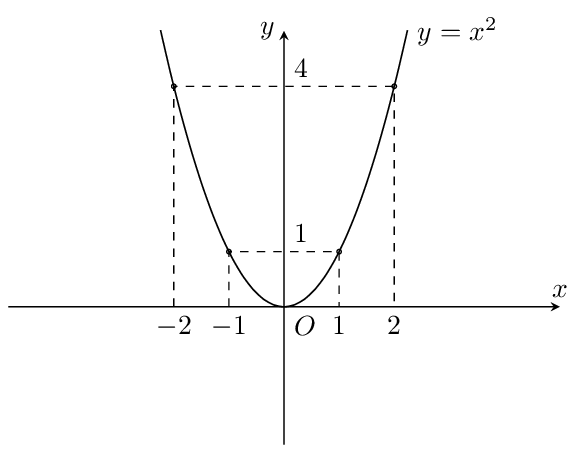
Ví dụ 1: Khảo sát và vẽ đồ thị hàm số $y=x^{2}$

Tập xác định: $ D=\mathbb{R}$

$ a=1>0$, hàm số đồng biến khi $ x>0$, hàm số nghịch biến khi $ x<0$

Bảng giá trị:

$ x$	$ -2$	$ -1$	$ 0$	$ 1$	$ 2$
$ y=x^{2}$	$ 4$	$ 1$	$ 0$	$ 1$	$ 4$

Đồ thị hàm số $ y=x^{2}$ là đường cong Parabol đi qua gốc tọa độ $ O$ và nhận $ Oy$ làm trục đối xứng.

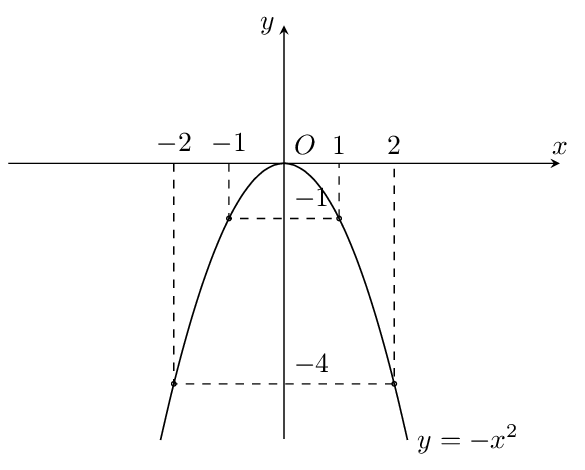
Ví dụ 2: Khảo sát và vẽ đồ thị hàm số $y=-x^{2}$

Tập xác định: $D=\mathbb{R}$

$a= -1<0 $, hàm số đồng biến khi $x<0$, hàm số nghịch biến khi $x>0$

Bảng giá trị:

$x$	$-2$	$-1$	$0$	$1$	$2$
$y= -x^2$	$-4$	$-1$	$0$	$-1$	$-4$

Đồ thị hàm số $y= -x^2$ là đường cong Parabol đi qua gốc tọa độ $O$ và nhận $Oy$ làm trục đối xứng.

Bài tập

Khảo sát và vẽ đồ thị hàm số bậc hai dưới đây:

a) $ \displaystyle y=\dfrac{1}{2}x^{2}$

b) $ \displaystyle y=-\dfrac{1}{2}x^{2}$

c) $ \displaystyle y=2x^{2}$

d) $ \displaystyle y=-2x^{2}$