ĐỊNH NGHĨA
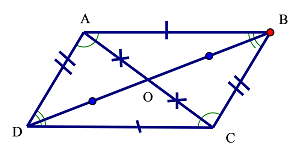
Hình bình hành ABCD
Hình bình hành là tứ giác có các cạnh đối song song. (AB // CD; AD // BC)
TÍNH CHẤT
Trong hình bình hành
+ Các góc đối bằng nhau (góc A = góc C; góc B = góc D)
+ Các cạnh đối bằng nhau (AB = CD; AD = BC)
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường (AC ∩ BD tại O; OA = OC; OB = OD).
DẤU HIỆU NHẬN BIẾT
– Tứ giác có các cạnh đối song song là hình bình hành.
– Tứ giác có các cạnh đối bằng nhau là hình bình hành.
– Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
– Tứ giác có các góc đối bằng nhau là hình bình hành.
– Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
BÀI TẬP
Bài 1: Khoanh vào chữ cái đứng trước câu trả lời đúng
Tứ giác ABCD là hình bình hành nếu:
A. AD// BC ; AC=BD B. AB=CD ;AC=BD
C. AB//CD; AD//BC D.AB=CD; AB//CD
Bài 2: Cho hình bình hành ABCD có chu vi bằng 10cm, chu vi tam giác ABD bằng 9cm. Tính BD
Bài 3: Tính các góc của hình bình hành ABCD biết:
$ a)\hat{A}={{100}^{o}}$
$ b)~\hat{A}-\hat{B}={{30}^{o}}$
Bài 4: Dựng hình bình hành ABCD biêý $ AB=4cm;AD=3cm;~\hat{A}={{60}^{o}}$
Bài 5: Cho tứ giác ABCD. Gọi M,N,P,Q theo thứ tự là trung điểm của AB, BC,CD,AD. Chứng minh rằng MNPQ là hình bình hành.
Bài 6: Cho hình bình hành ABCD. Gọi E là trung điểm của AD; F là trung điểm của BC. Chứng minh:
$ a)BE=DF$ và $ \widehat{{ABE}}=\widehat{{CDF}}~$
b)BE//DF
Gợi ý: Chứng minh $ \vartriangle ABE=\vartriangle CDF\left( {c.g.c} \right)$
Bài 7: Cho hình bình hành ABCD. Trên các cạnh AB, CD lần lượt lấy E,F sao cho AE=CF. Chứng minh rằng:
a) Tứ giác AECF là hình bình hành
b) BF//ED
c) Các đường thẳng AC;EF;BD đồng quy.
Bài 8: Cho hình bình hành ABCD. Gọi I, K lần lượt là trung điểm của các cạnh AB và CD. Gọi M và N lần lượt là giao điểm của AI và CK với BD. Chứng minh:
$ a)\vartriangle ADM=\vartriangle CBN$
$ b)\widehat{{MAC}}=\widehat{{NCA}}\And $$ IM//CN$
$ c)DM=MN=NB$
Bài 9: Cho hình bình hành ABCD. Vẽ AM vuông góc với BD tại M. AM cắt CD tại E. Vẽ CN vuông góc với BD tại N, CN cắt AB tại F. Chứng minh rằng:
a) Tứ giác AECF là hình bình hành
b) Tứ giác AMCN là hình bình hành
Bài 10: Cho hình bình hành ABCD (AB>BC). Tia phân giác của góc D cắt AB ở E. Tia phân giác của góc B cắt CD ở F.
a) Chứng minh $ DE//BF$
b) Tứ giác DEBF là hình gì?
Bài 11: Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, trên cạnh CD lấy điểm F sao cho EF//AD.
a) Chứng minh rằng: AE//DF; BE//CF.
b) Chứng minh tứ giác AEFD là hình bình hành
c) Chứng minh tứ giác BEFC là hình bình hành
Bài 12: Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, trên cạnh CD lấy điểm F sao cho AE=DF
a) Chứng minh rằng: AE//DF; BE//CF.
b) Chứng minh BE=DF
c) Chứng minh tứ giác AEFD là hình bình hành
d) Chứng minh tứ giác BEFC là hình bình hành
Bài 13: Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, trên cạnh CD lấy điểm F sao cho $ AE=CF$. Gọi O là giao điểm của AC và BD.
a) Chứng minh rằng tứ giác AECF là hình bình hành
b) Chứng minh rằng O là trung điểm của EF.
Bài 14: Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N ,P, Q lần lượt là trung điểm của các đoạn OA; OB; OC; OD.
a) Chứng minh rằng tứ giác MNPQ là hình bình hành
b) Chứng minh : Tứ giác ANCQ ; BPDM là các hình bình hành .
Bài 15: Cho hình thang ABCD $ \left( {AB//CD} \right)$. M là điểm nằm trong hình thang ABCD. Vẽ các hình bình hành MDEA,MCFB. Gọi I là giao điểm của AD và EM. K là giao điểm của BC và FM. Chứng minh rằng:
a) $ IK//EF$
b) $ EF=AB+CD$
Bài 16: Cho tứ giác ABCD có M là trung điểm cạnh BC, N là trung điểm cạnh CD, P là điểm thuộc cạnh BC $ \left( {PB\ne PC} \right)$, Q là điểm thuộc cạnh AD, $ \left( {QA\ne QD} \right)$. Biết MPNQ là hình bình hành. Chứng minh rằng $ BC//AD$
Bài 17:
a) Cho tam giác nhọn ABC, H là trực tâm của tam giác. Chứng minh rằng: $ AB+AC>AH+BH+CH$.Từ đó suy ra chu vi tam giác ABC lớn hơn $ \displaystyle \frac{3}{2}\left( {AH+BH+CH} \right)$
b) Cho hình bình hành ABCD. Xác định vị trí điểm M trong hình bình hành ABCD sao cho $ M{{A}^{2}}+M{{B}^{2}}+M{{C}^{2}}+M{{D}^{2}}$ đạt giá trị nhỏ nhất.
Bài 18: Cho tam giác ABC. M là một điểm nằm trong tam giác. Lần lượt vẽ các hình bình hành MBDC, MAED. Chứng minh khi điểm M di động thì đường thẳng ME luôn đi qua một điểm cố định.

