KIẾN THỨC CẦN NHỚ
Phương pháp: Ta trình bày phép chia này tương tự cách chia số tự nhiên. Với hai đa thức tùy ý $A$ và $B$ của cùng một biến, $B \neq 0$ tồn tại duy nhất hai đa thức Q và R sao cho:
$A=B \cdot Q+R$ (trong đó $R=0$ hoặc bậc của $R$ bé hơn bậc của $B$)
– Nếu $R=0\colon $ ta nói rằng đó là phép chia hết
– Nếu $R \neq 0\colon $ ta nói rằng đó là phép chia có dư.
*Chú ý:
a) Định lý Bơ-đu (Bézout): Cho đa thức bậc $n$ ẩn $x\colon $
$f(x)=a_{n} x^{n}+a_{n}-1 x^{n-1}+\ldots a_{1} x+a_{0}\left(a_{n} \neq 0\right) \cdot $
Số dư trong phép chia đa thức $f(x)$ cho nhị thức bậc nhất $(x-a)$ bằng giá trị của đa thức $f(x)$ tại $x=a \cdot $
b) Hệ quả: $f(x)$chia hết cho $(x-a)_{\mid}$ $\Leftrightarrow f(a)=0$
$f(a)$ là giá trị của đa thức $f(x)$ tại $x=a$, với $a$ là nghiệm của đa thức $f(x) \cdot $
c) Ta chứng minh được rằng:
Trong đa thức $f(x)=a_{n} x^{n}+a_{n}-1 x^{n-1}+\ldots a_{1} x+a_{0}\left(a_{n} \neq 0\right)$ với $a_{n,}$ $a_{n-1}, \ldots, a_{1} a_{0}$ là các số nguyên, nghiệm hữu tỉ (nếu có) phải có dạng $\displaystyle\frac{p}{q}$, trong đó $p$ là ước của hệ số tự do $\left(p / a_{0}\right)$ và $q$ là ước dương của hệ $q$
Số của hạng tử cao nhất $\left(q / a_{n}\right) \cdot $
BÀI TẬP VÍ DỤ
Ví dụ 1: Cho A và B là hai đa thức. Hãy chia A cho B rồi viết A dưới dạng:
$A=B \cdot Q+R$
$A=2 x^{3}-x^{2}-x+1 ; B=x^{2}-2 x \cdot $
Bài giải:
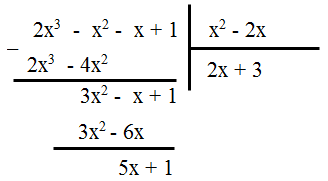
Vậy $2 x^{3}-x^{2}-x+1=\left(x^{2}-2 x\right)(2 x+3)+5 x+1$.
Ví dụ 2: Dùng hằng đẳng thức để làm tính chia $\left(x^{4}+2 x^{2} y^{2}+y^{2}\right)\colon \left(x^{2}+y^{2}\right)$
Bài giải:
Ta có: $\left(x^{4}+2 x^{2} y^{2}+y^{4}\right)\colon \left(x^{2}+y^{2}\right)$
$=\left(x^{2}+y^{2}\right)^{2}\colon \left(x^{2}+y^{2}\right)=x^{2}+y^{2}$.
BÀI TẬP VẬN DỤNG
BÀI TẬP CƠ BẢN
Bài 1: Làm tính chia
a) $\left(x^{3}+3 x^{2}-4\right)\colon (x-1)$
b) $\left(x^{4}-3 x^{2}+10 x-6\right)\colon \left(x^{2}-2 x+3\right)$
Bài giải:
a)
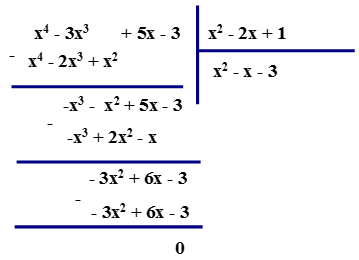
Vậy $x^{4}-3 x^{3}+5 x-3=\left(x^{2}-2 x+1\right) \cdot\left(x^{2}-x-3\right)$
b) $\left(x^{4}-3 x^{2}+10 x-6\right)\colon \left(x^{2}-2 x+3\right)$
Vậy $x^{4}-3 x^{2}+10 x-6=\left(x^{2}-2 x+3\right) \cdot\left(x^{2}+2 x-2\right)$
Bài 2: Tìm số b để đa thức $5 x^{3}+2 x^{2}-7 x+b$ chia hết cho $x-3 \cdot $
Bài giải:
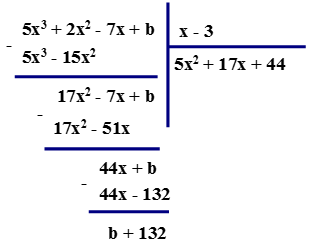
Để phép chia trên là phép chia hết thì $b+132=0 \Leftrightarrow b=-132 \cdot $
BÀI TẬP NÂNG CAO
Bài 1: Tìm m để đa thức $A(x)=3 x^{2}+m x+27$ chia cho đa thức $B(x)=x+5$ có dư bằng 2.
Bài giải:
Thực hiện phép tính:
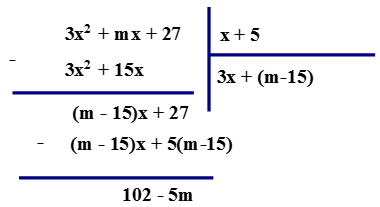
Từ điều kiện đề bài ta suy ra: $102-5 m=2 \Leftrightarrow 100=5 m \Leftrightarrow m=20 \cdot $
Vậy giá trị cần tìm là: $m=20 \cdot $
Bài 2: Tìm $n \in \mathbb{Z}$ để giá trị đa thức $6 n^{2}-n+5$ chia hết cho giá trị của đa thức $2 n+1 \cdot $
Bài giải:
Thực hiện phép chia ta được: $6 n^{2}-n+5=(2 n+1) \cdot(3 n-2)+7$
Vậy để giá trị của đa thức $6 n^{2}-n+5$ chia hết cho giá trị của đa thức $2 n+1$ thì 7 phải chia hết cho $2 n+1$.
$\Leftrightarrow 2 n+1$ là ước nguyên của 7.
| $2 n+1$ | $-7$ | $-1$ | $1$ | $7$ |
| $n$ | $-4$ | $-1$ | $0$ | $3$ |

