Tính tổng dãy số lũy thừa có quy luật

Để tính được tổng dãy số lũy thừa có quy luật thì cần phải có phương pháp giải. Đó là các phương pháp:

Công thức tổng lũy thừa cần nhớ

Với a ≠ 1:

1 + a + a² + … + aⁿ = (aⁿ⁺¹ − 1)/(a − 1).

Với tổng đổi dấu:

1 − a + a² − a³ + … + (−a)ⁿ = [1 − (−a)ⁿ⁺¹]/(1 + a), với a ≠ −1.

Khi nào nên dùng phương pháp nhân rồi trừ?

Nếu các số hạng liên tiếp hơn kém nhau một nhân tử cố định, hãy nhân toàn bộ tổng với nhân tử đó rồi trừ hai biểu thức. Phần lớn số hạng ở giữa sẽ triệt tiêu, chỉ còn số hạng đầu và cuối. Đây là cách nhanh để tự suy ra công thức thay vì học thuộc.

Trước khi áp dụng, cần kiểm tra dấu của các số hạng và số mũ đầu – cuối; sai một dấu ở bước trừ có thể làm sai toàn bộ kết quả.

PHƯƠNG PHÁP TÍNH

1. Phương pháp quy nạp

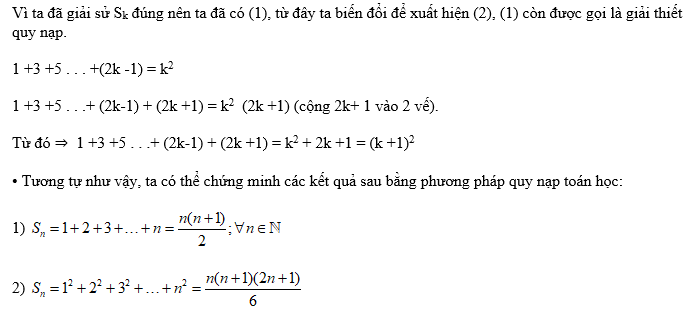
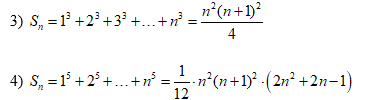
2. Sử dụng phương pháp khử liên tiếp tính tổng dãy số

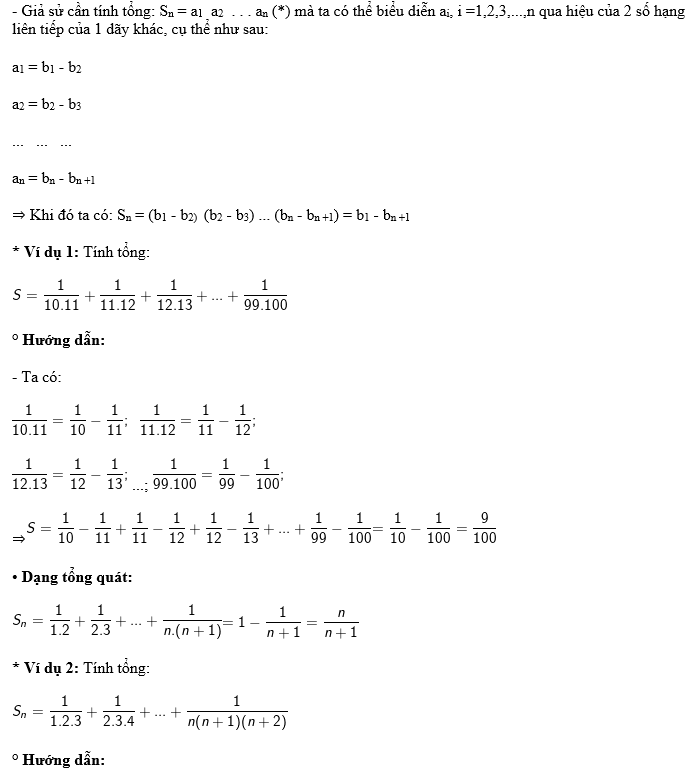
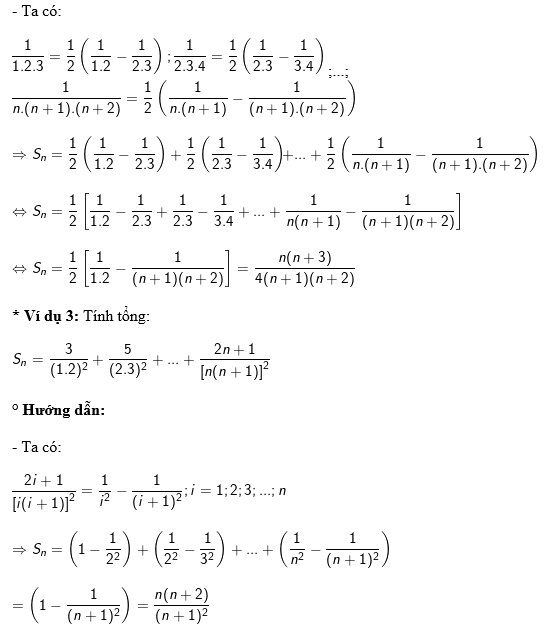
CÁC DẠNG TOÁN TÍNH TỔNG DÃY SỐ LŨY THỪA

Với các dạng toán dưới đây, các em dùng phương pháp tính nêu ở trên để áp dụng vào giải.

1. Dạng toán giải phương trình với ẩn là tổng cần tìm

Ví dụ 1: Tính tổng: S = 1+2 +2² + . . . +2¹⁰⁰ (*)

Hướng dẫn:

Cách 1: Ta viết lại S như sau:

S = 1+ 2(1 +2 +2² + . . .+ 2⁹⁹)

S = 1 + 2(1 + 2 + 2² + . . .+ 2⁹⁹ + 2¹⁰⁰ – 2¹⁰⁰)

⇒ S = 1 + 2(S – 2¹⁰⁰) = 1+2S – 2¹⁰¹

⇒ S = 2¹⁰¹ – 1

Cách 2: Nhân 2 vế với 2, ta được:

2S = 2(1 +2 +2² + . . . 2¹⁰⁰)

⇔ 2S = 2 +2² + 2³ + . . .+ 2¹⁰¹ (**)

– Lấy (**) trừ đi (*) ta được:

2S – S = (2 + 2² + 2³ + . . . +2¹⁰¹) – (1 +2 +2²  +. . . +2¹⁰⁰)

⇔ S = 2¹⁰¹ – 1.

Tổng quát cho dạng toán này như sau:

$S_{n}=1+a+a^{2}+\ldots+a^{n} ;(a, n \in \mathbb{N}, a>1, n \geq 1)$

Ta nhân cả 2 vế của S_n với a. Rồi TRỪ vế với vế ta được: $S_{n}=\dfrac{a^{n+1}-1}{a-1}$

Ví dụ 2: Tính:

S = 1 – 2 + 2² – 2³ + 2⁴ – . . . – 2⁹⁹ + 2¹⁰⁰

Hướng dẫn:

Ta có:

2S = 2(1 – 2 +2² – 2³ + 2⁴ – . . . – 2⁹⁹ + 2¹⁰⁰)

⇔ 2S = 2 – 2² + 2³ – 2⁴ + 2⁵ – . . . – 2¹⁰⁰ + 2¹⁰¹

⇔ 2S S = (2 – 2² + 2³ – 2⁴ + 2⁵ – . . . – 2¹⁰⁰ + 2¹⁰¹) (1 – 2 + 2² – 2³ + 2⁴ – . . . – 2⁹⁹ + 2¹⁰⁰)

⇔ 3S = 2¹⁰¹ + 1.

⇔ $S=\dfrac{2^{101}+1}{3}$

Tổng quát cho dạng toán này như sau:

$S_{n}=1-a+a^{2}-a^{3}+\ldots-a^{2 n-1}+a^{2 n} ;(a, n \in \mathbb{N}, a>1, n \geq 1)$

Ta nhân cả 2 vế của S_n với a. Rồi CỘNG vế với vế ta được: $S_{n}=\dfrac{a^{2 n+1}+1}{a+1}$

Ví dụ 3: Tính tổng:

S = 1+3² + 3⁴ + . . .+ 3⁹⁸ + 3¹⁰⁰ (*)

Hướng dẫn:

– Với bài toán này, mục tiêu là nhân 2 vế của S với một số nào đó mà khi trừ vế với vế thì ta được các số khử (triệt tiêu) liên tiếp.

– Đối với bài này, ta thấy số mũ của 2 số liên tiếp cách nhau 2 đơn vị nên ta nhân hai vế với 3² rồi áp dụng phương pháp khử liên tiếp.

S = 1+3² + 3⁴ + . . .+ 3⁹⁸ + 3¹⁰⁰

⇔ 3².S = 3²(1 +3² + 3⁴ + . . . +3⁹⁸ + 3¹⁰⁰)

⇔ 9S= 3² + 3⁴ + . . .+ 3¹⁰⁰ + 3¹⁰²  (**)

– Ta Trừ vế với vế của (**) cho (*) được:

9S-S= (3² + 3⁴ + . . . 3¹⁰⁰ + 3¹⁰²) – (1+3² +3⁴ + . . . +3⁹⁸ + 3¹⁰⁰)

⇔ 8S = 3¹⁰² – 1

⇔ $S=\dfrac{3^{102}-1}{8}$

• Tổng quát cho dạng toán này như sau:

$S_{n}=1+a^{d}+a^{2 d}+\ldots+a^{n d} ;(a, n, d \in \mathbb{N} ; a>1)$

Ta nhân cả 2 vế của S_n với a^d . Rồi TRỪ vế với vế ta được:

$S_{n}=\dfrac{a^{(n+1) d}-1}{a^{d}-1}$

Ví dụ 4: Tính:

S = 1 – 2³ + 2⁶ – 2⁹ . . . +2⁹⁶ – 2⁹⁹ (*)

Hướng dẫn:

– Lũy thừa các số liên tiếp cách nhau 3 đơn vị, nhân 2 vế với 2³ ta được:

2³.S =  2³.(1 – 2³ + 2⁶ – 2⁹ + . . .+ 2⁹⁶ – 2⁹⁹)

⇒ 8S = 2³ – 2⁶ + 2⁹ – 2¹² + . . . +2⁹⁹ – 2¹⁰² (**)

– Ta CỘNG vế với vế (**) với (*) được:

8S S = (2³ – 2⁶ + 2⁹ – 2¹² + . . . +2⁹⁹ – 2¹⁰²) (1 – 2³ + 2⁶ – 2⁹ + . . .+ 2⁹⁶ – 2⁹⁹)

⇔ 9S = 1 – 2¹⁰² ⇔ $S=\dfrac{1-2^{102}}{9}$

Tổng quát cho dạng toán này như sau:

$S_{n}=1-a^{d}+a^{2 d}-a^{3 d}+\ldots+a^{n d} ;(a, n, d \in \mathbb{N} ; a>1)$

Ta nhân cả 2 vế của S_n với a^d . Rồi CỘNG vế với vế ta được:

$S_{n}=\dfrac{1-a^{(n+1) d}}{a^{d}+1}$

2. Dạng toán vận dụng công thức tính tổng các số hạng của dãy số cách đều

Để đếm được số hạng của 1 dãy số mà 2 số hạng liên tiếp cách đều nhau 1 số đơn vị ta dùng công thức:

 Số số hạng = [(số cuối – số đầu) : (khoảng cách)] + 1

Để tính Tổng các số hạng của một dãy mà 2 số hạng liên tiếp cách đều nhau 1 số đơn vị ta dùng công thức:

Tổng = [(số đầu + số cuối) . (số số hạng)] : 2

Ví dụ 1: Tính tổng: S = 1+3+5 +7 +… +39

Hướng dẫn:

Số số hạng của S là: (39-1):2+1 = 19+1 = 20.

Tổng S = [20.(39+1)]:2 = 10.40 = 400.

Ví dụ 2: Tính tổng: S = 2+5+8+…+59

Hướng dẫn:

Số số hạng của S là: (59-2):3+1 = 19+1 = 20.

Tổng S = [20.(59+2)]:2 = 10.61 = 610.

3. Dạng toán tổng hợp vận dụng các tổng đã biết

Ký hiệu: $\sum_{i=1}^{n} a_{i}=a_{1}+a_{2}+\ldots+a_{n}$

Tính chất:

$\sum_{i=1}^{n}\left(a_{i}+b_{i}\right)=\sum_{i=1}^{n} a_{i}+\sum_{i=1}^{n} b_{i}$

$\sum_{i=1}^{n} a \cdot a_{i}=a \sum_{i=1}^{n} a_{i}$

Ví dụ: Tính tổng: S_n = 1.2+2.3 +3.4 … n(n+1)

Hướng dẫn:

Ta có: $S_{n}=\sum_{i=1}^{n} i(i+1)=\sum_{i=1}^{n}\left(i^{2}+i\right)=\sum_{i=1}^{n} i^{2}+\sum_{i=1}^{n} i$

Mặt khác, lại có:

$\sum_{i=1}^{n} i=1+2+3+\ldots+n=\dfrac{n(n+1)}{2}$ (theo PP quy nạp ở mục I).

$\sum_{i=1}^{n} i^{2}=\dfrac{n(n+1)(n+2)}{6}$ (theo PP quy nạp ở mục I)

⇒ $S_{n}=\dfrac{n(n+2)}{2}+\dfrac{n(n+1)(n+2)}{6}=\dfrac{n(n+1)(n+2)}{3}$

BÀI TẬP VẬN DỤNG

Bài 1: Tính tổng: S = 3 + 8 + 13 + 18 + … + 228

Bài 2: Tính các tổng sau:

a) S = 6 +6² + 6³ + … +6⁹⁹ + 6¹⁰⁰

b) S = 5 +11 +17 … + 95 +101

c) $S=\dfrac{1}{1\cdot 2}+\dfrac{1}{23}+\dfrac{1}{3\cdot 4} \ldots+\dfrac{1}{49\cdot 50}$

d) $S=\dfrac{6}{5\cdot 7}+\dfrac{6}{79}+\dfrac{6}{9\cdot 11}+\ldots+\dfrac{6}{57\cdot 59}$

Bài 3: Chứng minh

a) 1.4 +4.7 +7.10 … + (3n-2)(3n+1) = n(n+1)²

b) $\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\ldots+\dfrac{1}{2^{0}}=1-\dfrac{1}{20}$