A. Tóm tắt lý thuyết Hình học lớp 6 học kì 1
1. Trong ba điểm thẳng hàng có một và chỉ một điểm nằm giữa hai điểm còn lại.
2. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
3. Mỗi điểm trên đường thẳng là gốc chung của hai tia đối nhau.
4. Nếu điểm $M$ nằm giữa hai điểm $A$ và $B$ thì $AM+MB=AB$.
5. Trung điểm $M$ của đoạn thẳng $AB$ là điểm nằm giữa $A, B$ và $MA=MB$.
B. Tóm tắt lý thuyết Hình học lớp 6 học kì 2
I. Các tính chất:
1. Bất kì đường thẳng nào nằm trên mặt phẳng cũng là bờ chung của hai nửa mặt phẳng đối nhau.
2. Số đo của góc bẹt bằng $180^{\circ}$.
3. Nếu tia Oy nằm giữa hai tia $Ox$ và $Oz$ thì $\widehat{xOy}+\widehat{yOz}=\widehat{xOz}$.
II. Các định nghĩa:
1. Tia phân giác của một góc
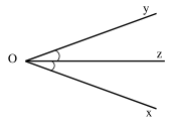
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.
2. Đường tròn
Đường tròn tâm $\mathrm{O}$, bán kính $R$ là hình gồm các điểm cách đều $O$ một khoảng bằng $R$, kí hiệu $(O ; R)$.
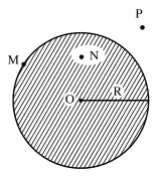
M là điểm nằm trên (thuộc) đường tròn. $N$ là điểm nằm bên trong đường tròn. $P$ là điểm nằm bên ngoài đường tròn.
Hình tròn là hình gồm các điểm nằm trên đường tròn và các điểm nằm bên trong đường tròn đó.
*Cung và dây cung
– Đoạn thẳng nối hai mút của cung là dây cung (gọi tắt là dây). Dây đi qua tâm là đường kính.
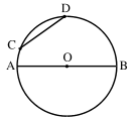
Trên hình vẽ, ta có $CD$ và $AB$ là các dây cung, $AB$ đi qua tâm $O$ nên $AB$ còn gọi là đường kính. Đường kính dài gấp đôi bán kính.
3. Tam giác
Tam giác ABC là hình gồm ba đoạn thẳng $AB, BC, CA$ khi ba điểm $A, B, C$ không thẳng hàng.
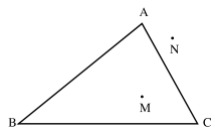
Tam giác ABC
Ba đoạn thẳng $AB, BC, CA$ là ba cạnh của tam giác.
Ba góc $ \displaystyle \widehat{{BAC}},\widehat{{CBA}},\widehat{{ACB}}$ là ba góc của tam giác.
Tam giác $ABC$ được kí hiệu là $\Delta ABC$. Ta còn gọi tên và kí hiệu tam giác $ABC$ là $\Delta BCA, \Delta CAB, \Delta ACB, \Delta CBA, \Delta BAC$.
Ba điểm $A, B, C$ là ba đỉnh của tam giác.
Trên hình vẽ, điểm $M$ là điểm nằm bên trong tam giác, điểm $N$ là điểm nằm bên ngoài tam giác.

