PHƯƠNG PHÁP GIẢI
Áp dụng Định lí thuận về tia phân giác.
Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
BÀI TẬP MINH HỌA
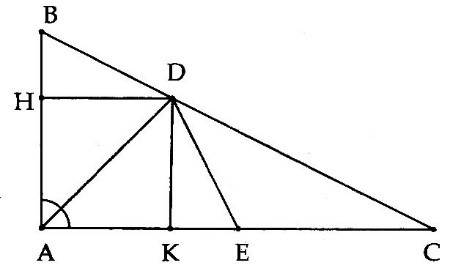
1A. Cho $ \displaystyle \Delta $ABC vuông tại A có AB = 3cm, AC = 6cm. Gọi E là trung điểm AC, tia phân giác của $ \displaystyle \widehat{A}$ cắt BC tại D.
a) Tính BC.
b) Chứng minh: $ \displaystyle \Delta $BAD = $ \displaystyle \Delta $
c) Gọi H, K lần lượt là hình chiếu của D trên AB, AC. Chứng minh điểm D cách đều AB và AC.
1B. Cho $ \displaystyle \widehat{{xOy}}$ khác 180°. Trên tia phân giác Ot của $ \displaystyle \widehat{{xOy}}$ lấy điểm M bất kì. Chứng minh điểm M cách đều Ox và Oy.
2A. Cho $ \displaystyle \Delta $ABC có $ \displaystyle \widehat{A}$ = 120°. Tia phân giác của A cắt BC tại D. Tia phân giác của $ \displaystyle \widehat{{ADC}}$ cắt AC tại I. Gọi H, K, E lần lượt là hình chiếu của I trên đương thẳng AB, BC, AD. Chứng minh:
a) AC là tia phân giác của $ \displaystyle \widehat{{DAH}}$.
b) IH = IK
2B. Cho $ \displaystyle \Delta $ABC. Hai tia phân giác của góc ngoài tại đỉnh B và đỉnh C cắt nhau tại I. Chứng minh điểm I cách đều hai cạnh AB, AC.
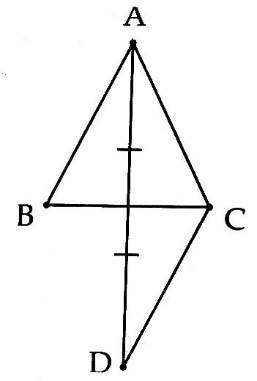
3A. Cho $ \displaystyle \Delta $ABC có trung tuyến AM đồng thời là đường phân giác. Trên tia AM lấy điểm D sao cho MD = MA. Chứng minh:
a) AB = CD.
b) $ \displaystyle \Delta $ACD cân tại C.
c) Chứng minh $ \displaystyle \Delta $ABC cân tại A.
3B. Cho tam giác ABC vuông tại A. Từ một điểm K bất kì trên cạnh BC, vẽ KH $ \displaystyle \bot $AC (H$ \displaystyle \in $AC). Trên tia đối của tia HK lấy điểm I sao cho HI = HK. Chứng minh:
a) Chứng minh AB //HK;
b) Chứng minh $ \displaystyle \widehat{{KAH}}=\widehat{{IAH}}$
c) Chứng minh $ \displaystyle \Delta $AKI cân,
HƯỚNG DẪN GIẢI
1A. a) Áp dụng Định lí Pytago trong tam giác vuông ABC tính, được BC $ \displaystyle \sqrt{{45}}$ cm.
Vì E là trung điểm AC nên
AE = $ \displaystyle \dfrac{1}{2}$AC = 3 cm => AE = AB
=> $ \displaystyle \Delta $BAD =$ \displaystyle \Delta $EAD (c.g.c).
c) Do DH $ \displaystyle \bot $AB nên DH là khoảng cách từ D đến AB.
Tương tự DK là khoảng cách từ D đến AC.
Suy ra DH = DK.
1B. Hạ ME, MF lần lượt vuông góc với Ox,Oy (E$ \displaystyle \in $Ox, F$ \displaystyle \in $ Oy). Chứng minh được $ \displaystyle \Delta $OME = $ \displaystyle \Delta $OMF (ch-gn) => ME = MF. Vậy M cách, đều hai cạnh Ox, Oy.
2A. a) Vì $ \displaystyle \widehat{{BAC}}$= 120° nên $ \displaystyle \widehat{{CAH}}$ = 60°.
Do AD là phân giác $ \displaystyle \widehat{{BAC}}$ nên
$ \displaystyle \widehat{{DAC}}=\dfrac{1}{2}\widehat{{BAC}}$ = 60°
=> $ \displaystyle \widehat{{DAC}}=\widehat{{CAH}}$
=> AC là phân giác $ \displaystyle \widehat{{DAH}}$.
b) Khi đó IE = IH.
Mặt khác DI là phân giác $ \displaystyle \widehat{{ADC}}$ nên IE = IK.
Vậy IH = IK.
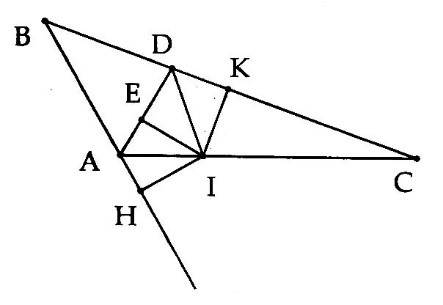
2B. Gọi E, F, P lần lượt là hình chiếu của I trên các đường thẳng AB, BC, CA.
Theo Định lí thuận ta có IE = IF và IF = IP => IE = IP .
Vậy I cách đều hai cạnh AB, AC.
3A. a) Trên tia đối của tia MA lấy D sao cho MA = MD.
=> $ \displaystyle \Delta $MAB = $ \displaystyle \Delta $MDC (c.g.c) => AB = CD
b) AM là phân giác $ \displaystyle \widehat{{BAC}}$ nên $ \displaystyle \widehat{{BAM}}=\widehat{{CAM}}$
Lại có $ \displaystyle \widehat{{BAM}}=\widehat{{CDM}}$ (hai góc tương ứng bằng nhau).
Do đó $ \displaystyle \widehat{{CAM}}=\widehat{{CDM}}$=> $ \displaystyle \Delta $CAD cân tại C => CA = CD.
c) Vậy AB = AC => $ \displaystyle \Delta $ABC cân tại A
3B. a) Ta có: AB $ \displaystyle \bot $ AC, KH $ \displaystyle \bot $AC
=> AB // KH.
b) $ \displaystyle \Delta $AHK = $ \displaystyle \Delta $AHI (ch-cgv)
=> $ \displaystyle \widehat{{KAH}}=\widehat{{IAH}}$.
c) $ \displaystyle \Delta $AKI có AH vừa là đường trung tuyến, vừa là đường phân giác nên $ \displaystyle \Delta $AKI cân tại A.

