PHƯƠNG PHÁP GIẢI
- Sử dụng tính chất đường trung trực để thay đổi độ dài một đoạn thẳng bằng độ dài một đoạn thẳng khác bằng nó.
- Sử dụng bất đẳng thức tam giác để tìm giá trị nhỏ nhất, giá trị lớn nhất.
BÀI TẬP MINH HỌA
9A. Hai điểm A, B cùng nằm trên nửa mặt phẳng có bờ là đường thẳng d. Tìm vị trí điểm C trên đường thẳng d sao cho giá trị của tổng CA + CB là nhỏ nhất.
9B. Hai nhà máy được xây dựng tại hai địa điểm A và B cùng nằm về một phía của khúc sông thẳng. Tìm trên bờ sông một địa điểm C để xây trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ C đến A và đến B là nhỏ nhất.
HƯỚNG DẪN GIẢI
9A. Lấy D là điểm đối xứng, với A qua d. Theo tính chất đường trung trực: CA = CD.
Do đó CA + CB = CD + CB.
Gọi M là giao điểm của BD và d.
Nếu C không trùng với M thì xét
$ \displaystyle \Delta $BCD, ta có: CB + CD > BD hay
CA + CB > BD (1).
Nếu C trùng với M thì:
CA + CB = MA + MB = MD + MB = BD (2).
So sánh (1) và (2) ta thấy điểm C trùng M hay C là giao điểm của BD và d thì giá trị của tổng CA + CB là nhỏ nhất.
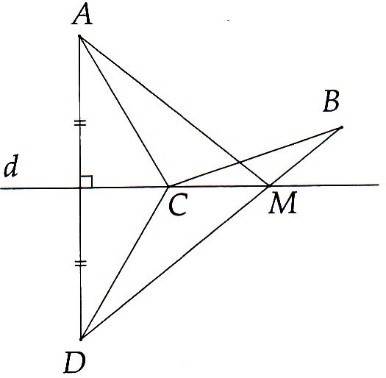
Chú ý: Điểm C tìm được ở vị trí M như vậy là điểm duy nhất. Thật vậy, nếu lấy E đối xứng với B qua d thì AE vẫn cắt d ở M đúng vị trí mà BD cắt d.
9B. Tương tự 9A.

