LÝ THUYẾT CĂN THỨC BẬC HAI
Kiến thức cần nhớ:
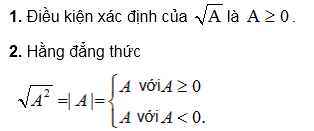
Các ví dụ:
Ví dụ 1: Tìm các giá trị của x để các biểu thức sau có nghĩa:
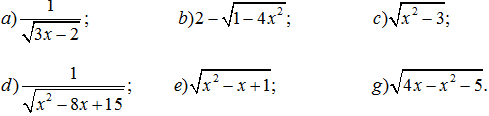
Giải
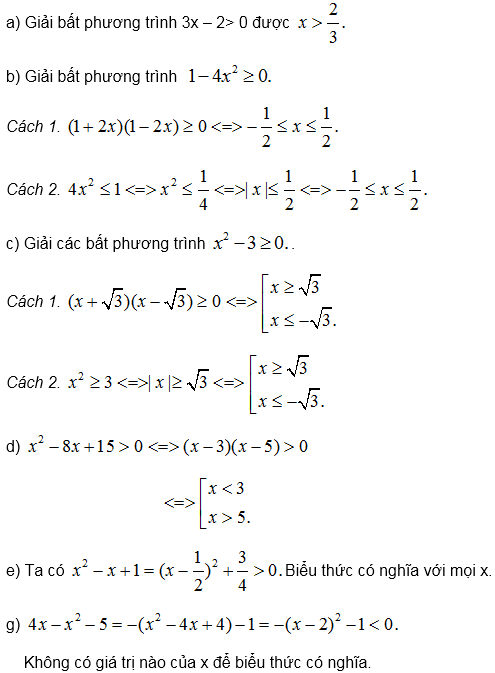
*Chú ý:
Muốn tìm các giá trị của x để biểu thức $\sqrt{A}$ có nghĩa, ta phải giải bất phương trình A ≥ 0.
Nếu A là nhị thức bậc nhất (câu a), ta phải giải bất phương trình bậc nhất một ẩn.
Nếu A là đa thức bậc hai (các câu còn lại), ta phải giải bất phương trình bậc hai (xem ví dụ 40). Ta chú ý các dạng sau :
a) Nếu A phân tích được thành nhân tử (các câu b, c, d) ta giải bất phương trình tích bằng xét dấu các nhị thức bậc nhất.
Trường hợp bất phương trình có dạng $x^{2} \leq \mathrm{a}$ (câu b) hoặc $x^{2} \geq a$ (câu c) trong đó a là hằng số dương, ta có thể giải thích bằng cách:
$x^{2} \leq a<=>|x| \leq \sqrt{a}<=>-\sqrt{a} \leq x \leq \sqrt{a}$
$ x^{2}\ge a<=>|x|\ge \sqrt{a}\Leftrightarrow \left[ {\begin{array}{*{20}{l}} {x\ge \sqrt{a}} \\ {x\le -\sqrt{a}} \end{array}} \right.$
b) Nếu A không phân tích được thành nhân tử (các câu e, g), ta sẽ chứng tỏ rằng biểu thức A :
– Luôn luôn có giá trị dương (khi đó $\sqrt{A}$ có nghĩa với mọi x) ;
– Hoặc luôn luôn có giá trị âm (khi đó $\sqrt{A}$ không có nghĩa với mọi x).
Ví dụ 2: Cho biểu thức $A=3 x-1-\sqrt{4 x^{2}+9-12 x}$
a) Rút gọn biểu thức A.
b) Tìm giá trị của x để A = 3.

BÀI TẬP
1. Tìm giá trị của x để các biểu thức sau có nghĩa:
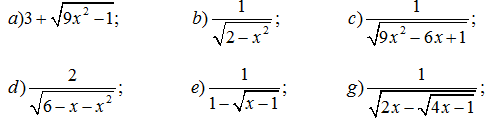
2. Rút gọn các biểu thức:
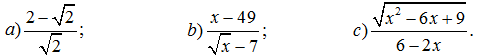
3. Rút gọn các biểu thức:
![]()
4. Với các giá trị nào của a và b thì: $\sqrt{a^{2}\left(b^{2}-2 b+1\right)}=a(1-b)$
5. Rút gọn biểu thức $A=2 x-1-\sqrt{x^{2}-x+\dfrac{1}{4}}$ rồi tìm giá trị của $x$ để $A=\dfrac{3}{2}$
6. Giải các phương trình:
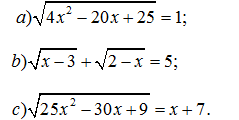
7. Tìm giá trị nhỏ nhất của biểu thức: $A=\sqrt{4 x^{2}-4 x+1}+\sqrt{4 x^{2}-12 x+9}$.

