Cách vẽ thêm hình để giải bài toán về đường tròn

Có những bài toán liên quan tới đường tròn khi chúng ta vẽ thêm yếu tố phụ thì việc giải bài toán sẽ trở nên dễ dàng hơn.

A. Những cách vẽ thêm yếu tố phụ

Những cách mà chúng ta thường làm trong các bài toán liên quan tới đường tròn là:

1. Vẽ đường kính vuông góc với một dây

Khi phải tính độ dài của một dây ta thường vẽ đường kính vuông góc với một dây để vận dụng định lí đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

Để chứng minh hai dây bằng nhau (hoặc không bằng nhau) ta cũng vẽ các đường kính vuông góc với hai dây đó.

* Chú ý: Vẽ đường kính đi qua trung điểm của dây cũng dẫn tới đường kính vuông góc với dây đó.

2. Vẽ bán kính đi qua tiếp điểm

Tiếp tuyến của đường tròn thì vuông góc với bán kính đi qua tiếp điểm. Vì vậy trong các bài toán có tiếp tuyến của đường tròn ta thường vẽ bán kính đi qua tiếp điểm, khi đó bán kính này vuông góc với tiếp tuyến.

3. Vẽ đường tiếp tuyến chung tại tiếp điểm của hai đường tròn tiếp xúc

Khi bài toán có cho hai đường tròn tiếp xúc, nếu cần ta có thể vẽ thêm một tiếp tuyến chung tại tiếp điểm. Điều này giúp ta có thể vận dụng được tính chất giao điểm hai tiếp tuyến của một đường tròn hoặc những tính chất khác sẽ thấy ở chương sau.

4. Vẽ dây chung của hai đường tròn cắt nhau

Nếu hai đường tròn cắt nhau thì dây chung vuông góc với đường nối tâm và bị đường nối tâm chia đôi. Vì vậy, nếu bài toán cho hai đường tròn cắt nhau ta có thể vẽ thêm dây chung để được hai đường thẳng vuông góc hoặc hai đoạn thẳng bằng nhau. Từ đó, tiếp tục vận dụng để chứng minh những điều khác. Dây chung đóng vai trò là yếu tố trung gian chuyển từ đường tròn này sang đường tròn kia.

B. Các bài toán vẽ thêm hình trong đường tròn

Các em tham khảo ví dụ dưới đây để học.

Ví dụ 1: Cho đường tròn (O; 2cm) và một điểm A sao cho OA = 3 cm. Một cát tuyến quay quanh A cắt đường tròn tại M và N. Tính giá trị lớn nhất của tổng AM + AN

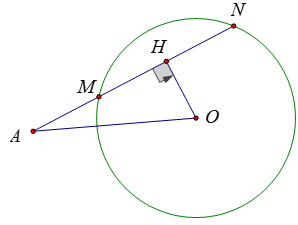
Hướng dẫn:

Vẽ OH ⊥ MN thì HM = HN

Ta có: AM = AH – HM và AN = AH + MN

Suy ra: AM + AN = AH – HM + AH + MN = 2AH ( do HM = HN)

Mặt khác AH ≤ AO ( quan hệ giữa đường vuông góc và đường xiên)

Do đó AM + AN ≤ 2 AO = 6 cm

Dấu bằng xảy ra khi cát tuyến AMN đi qua O

Vậy giá trị lớn nhất của tổng AM + AN là 6 cm, khi cát tuyến đi qua O

Ví dụ 2: Cho góc xOy có số đo bằng 60⁰ . Lấy điểm E trên tia phân giác của góc đó. Vẽ đường tròn (E) cắt tia Ox tại A và B, cắt tia Oy tại C và D sao cho OA < OB ; OC < OD. Vẽ đường tròn (F) đi qua 3 điểm E, A, D. Chứng minh rằng

a) AB = CD

b) góc AED bằng 120⁰

c) F thuộc đường tròn (E)

Hướng dẫn:

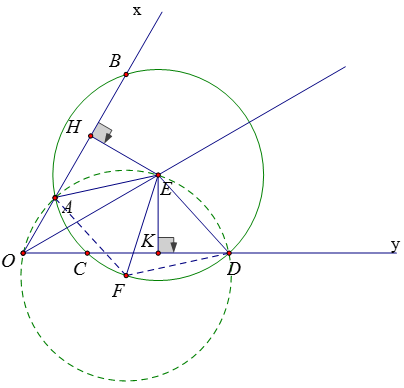
a) Vẽ EH ⊥ AB; EK ⊥ CD

Theo tính chất tia phân giác, ta có: EH = EK

⇒ AB = CD (hai dây cách đều tâm thì bằng nhau)

b) ΔHEA= ΔKED (cạnh huyền – cạnh góc vuông)

$\Rightarrow \breve{\mathrm{HEA}}=\widehat{\mathrm{KED}}$
$\Rightarrow \widehat{\mathrm{HEA}}+\widehat{\mathrm{AEK}}=\widehat{\mathrm{AEK}}+\widehat{\mathrm{KED}}$ hay $\widehat{\mathrm{AED}}=\widehat{\mathrm{HEK}}$

Mặt khác:

$\widehat{\mathrm{HEK}}=180^{\circ}-60^{\circ}=120^{\circ}$
$\Rightarrow \widehat{\mathrm{AED}}=120^{\circ}$

c) ΔAEF= ΔDEF (c.c.c)

$\Rightarrow \widehat{\mathrm{AEF}}=\widehat{\mathrm{DEF}}=\dfrac{1}{2} \widehat{\mathrm{AED}}=\dfrac{1}{2} \cdot 120^{\circ}=60^{\circ}$

ΔAEF có FA = FE nên là tam giác cân, lại có góc AEF bằng 60⁰ nên là tam giác đều.

Vậy điểm F thuộc đường tròn (E).

Ví dụ 3: Từ một điểm A ở bên ngoài hai đường tròn đồng tâm (O) vẽ hai tiếp tuyến AM, AN với đường tròn nhỏ (M, N là các tiếp điểm). Tia AM cắt đường tròn lớn tại B và C (B nằm giữa A và C), tia AN cắt đường tròn lớn tại D và E (D nằm giữa A và E). Chứng minh rằng:

a) Tam giác ACE cân

b) Tứ giác BDEC là hình thang cân.

Hướng dẫn:

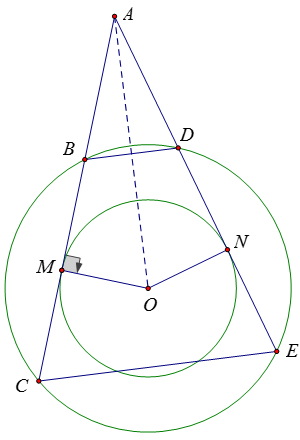
a) Nối OM, ON. Vì AM, AN là hai tiếp tuyến nên

OM ⊥ AM; ON ⊥ AN; AM = AN

Vì OM = ON nên BC = DE

Mặt khác, ta có:

MB = MC = 1/2 BC và ND = NE = 1/2 DE

Nên AM + MC = AN + NE ⇔ AC = AE

Vậy ΔACE cân.

b) Ta có: AC = AE; BC = DE

⇒ AC – BC = AE – DE hay AB = AD

Hai tam giác cân ABD và ACE có chung góc A ở đỉnh nên góc ABD bằng góc ACE do đó BD // CE

⇒ Tứ giác BDEC là hình thang

Lại có góc C bằng góc E nên tứ giác BDEC là hình thang cân.

Ví dụ 4: Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài với nhau tại A. Vẽ tiếp tuyến chung ngoài BC với B ∈ (O); C ∈ (O’). Chứng minh rằng $B C=2 \sqrt{R \cdot R^{\prime}}$.

Hướng dẫn:

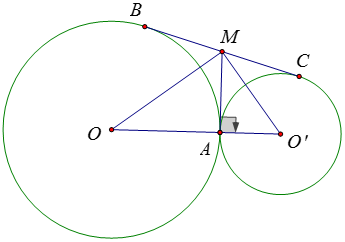
Qua A vẽ tiếp tuyến chung của hai đường tròn cắt BC tại M.

Ta có: AM ⊥ OO’ và AM = BM = CM = 1/2 BC

Các tia MO và MO’ là các tia phân giác của hai góc kề bù góc AMB và góc AMC nên MO ⊥ MO’

Xét tam giác OMO’ vuông tại M có MA là đường cao:

MA² = OA.O’A

$\Rightarrow \mathrm{MA}=\sqrt{\mathrm{R} \cdot \mathrm{R}^{\prime}}$
Mà $\mathrm{BC}=2 \mathrm{MA}=2 \sqrt{\mathrm{R} \cdot \mathrm{R}^{\prime}}$

Ví dụ 5: Cho nửa đường tròn (O) đường kính AB. Vẽ bán kính OC ⊥ AB rồi từ C vẽ tiếp tuyến xy với nửa đường tròn. Vẽ đường tròn (K) tiếp xúc với AB và tiếp xúc trong với đường tròn (O). Chứng minh rằng tâm K luôn cách đều điểm O và đường thẳng xy

Hướng dẫn:

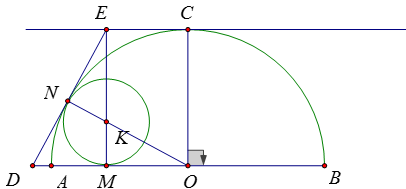
Gọi M, N lần lượt là tiếp điểm của đường tròn (K) với AB và với đường tròn (O)

Từ N vẽ một tiếp tuyến chung với hai đường tròn, nó cắt đường thẳng AB tại D và cắt đường thẳng MK tại E.

Ta sẽ chứng minh E thuộc đường thẳng xy

Ta có 3 điểm K, O, N thẳng hàng và KN ⊥ DE; C và DM = DN

ΔMDE= ΔNDO (g.c.g)

⇒ EM = ON, do đó EM = OC = R, dẫn tới E ∈ xy và KE ⊥ xy (vì xy // AB)

ΔNKE = ΔMKO (g.c.g)

⇒ KE = KO

Vậy tâm K luôn cách đều điểm O và đường thẳng xy

Ví dụ 6: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ một cát tuyến EAF trong đó E ∈ (O) và F ∈ (O’). Chứng minh rằng đường trung trực của EF luôn đi qua một điêm cố định.

Hướng dẫn:

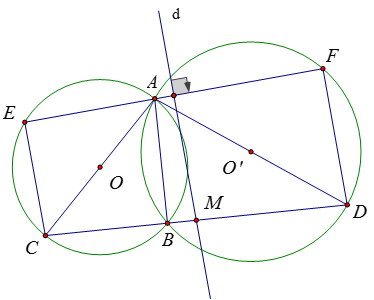
Vẽ dây chung AB và các đường kính AOC và AO’D

Ta được: $\widehat{\mathrm{ABC}}=90^{\circ} ; \widehat{\mathrm{ABD}}=90^{\circ}$ do đó, 3 điểm B, C, D thẳng hàng và CD là một đoạn thẳng cố định

Ta có: $\widehat{\mathrm{AEC}}=90^{\circ} ; \widehat{\mathrm{AFD}}=90^{\circ}$ nên EC // FD

⇒ Tứ giác FECD là hình thang vuông.

Đường thẳng (d) là đường trung trực của EF nên d // EC // FD do đó (d) đi qua trung điểm của CD, đó là một điểm cố định.