Hiểu rõ về số gần đúng và sai số

1. Số gần đúng

Trong nhiều trường hợp, ta không biết được giá trị đúng của đại lượng mà ta đang quan tâm mà chỉ có thể biết được giá trị gần đúng của nó.

Ví dụ 1: Các số liệu sau là những số gần đúng:

– Khoảng cách từ Mặt Trăng đến Trái Đất là 384400km.

-Số dân của Việt Nam (theo số liệu năm 2005) là 83 triệu người.

2. Sai số

a. Sai số tuyệt đối và độ chính xác d:

Nếu $ a$ là số gần đúng của số $ \bar{a}$thì $ \Delta $($ a$)= $ \left| {\bar{a}-a\left. {} \right|} \right.$được gọi là sai số tuyệt đối của số gần đúng $ a$.

Thông thường ta không biết được số đúng  $ \bar{a}$nên cũng không  tính được $ \Delta (a)$mà chỉ ước lượng được $ \Delta (a)$không vượt quá một số dương nào đó.

Khi đó $ \Delta (a)\le d\Leftrightarrow -d\le \bar{a}-a\le d\Leftrightarrow a-d\le \bar{a}\le a+d$ điều đó có nghĩa là số đúng $ \bar{a}$dao động từ $ a-d$đến $ a+d$và do đó ta nói $ a$là số gần đúng của $ \bar{a}$với độ chính xác $ d$quy ước viết gọn là $ \bar{a}=a\pm d$.

Ví dụ 2: Kết quả đo chiều dài của một cây cầu được ghi là $ 152m\pm 0,2m$, điều đó có nghĩa là gì?

Giải

Kết quả đo chiều dài của một cây cầu được ghi là $ 152m\pm 0,2m$có nghĩa là chiều dài đúng của cây cầu là một số nằm trong khoảng từ $ 151,8m$đến $ 152,2m$.

Ví dụ 3: Khi tính diện tích hình tròn bán kính R = 3cm, nếu lấy $ \pi =3,14$thì độ chính xác là bao nhiêu?

Giải

Ta có diện tích hình tròn S = 3,14. 3² và $ \displaystyle \bar{S}=\pi .3^{2}=9\pi $

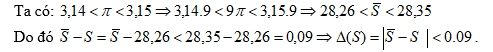
Vậy nếu ta lấy $ \pi =3,14$ thì diện tích hình tròn là S = 28,26cm² với độ chính xác $ d=0,09$.

b. Sai số tương đối

Sai số tương đối của số gần đúng $ a$là $ \delta (a)=\dfrac{{\Delta (a)}}{{\left| {a\left. {} \right|} \right.}}$

Nếu $ \bar{a}=a\pm d$thì $ \Delta (a)\le d$. Do đó $ \delta (a)\le \dfrac{d}{{\left| {a\left. {} \right|} \right.}}$

Nếu $ \dfrac{d}{{\left| a \right|}}$càng nhỏ thì chất lượng của phép đo đạc càng cao.

Người ta thường viết sai số tương đối dưới dạng phần trăm.

Ví dụ 4: Tìm sai số tương đối của phép đo chiều dài cây cầu ở Ví dụ 2.

Giải

Trong phép đo chiều dài cây cầu ở Ví dụ 2 thì sai số tương đối không vượt quá $ \dfrac{{0,2}}{{152}}=0,1316\%$

Ví dụ 5: Bạn A đo chiều dài của một sân bóng ghi được $ 250\pm 0,2m$. Bạn B đo chiều cao của một cột cờ được $ 15\pm 0,1m$. Trong 2 bạn A và B, bạn nào có phép đo chính xác hơn?

Giải

Phép đo của bạn A có sai số tương đối $ \delta _{1}\le \dfrac{{0,2}}{{250}}=0,0008=0,08\%$

Phép đo của bạn B có sai số tương đối $ \delta _{2}\le \dfrac{{0,1}}{{15}}=0,0066=0,66\%$