Viết phương trình đường thẳng đi qua 2 điểm là dạng bài tập cơ bản trong chương trình Toán 10 mà các em học sinh lớp 10 cần phải nắm được.
LÝ THUYẾT CẦN NHỚ
Phương trình tổng quát của đường thẳng
Đường thẳng Δ có phương trình tổng quát là: $a x+b y+c=0 ;\left(a^{2}+b^{2} \neq 0\right)$ nhận $\vec{n}=(a ; b)$ làm vectơ pháp tuyến.
Phương trình tham số của đường thẳng
– Phương trình tham số của đường thẳng đi qua điểm $A\left(x_{0}, y_{0}\right)$ nhận $\vec{u}=(a ; b)$ làm vecto chỉ phương, Ta có:
$B(x, y) \in d \Leftrightarrow \overrightarrow{A B}=t \vec{u} \Leftrightarrow\left\{\begin{array}{l}x-x_{0}=a t \\ y-y_{0}=b t\end{array}\right.$
$\Leftrightarrow\left\{\begin{array}{l}x=x_{0}+a t \\ y=y_{0}+b t\end{array} ;\left(a^{2}+b^{2} \neq 0, t \in \mathbb{R}\right)\right.$
– Đường thẳng d đi qua điểm $A\left(x_{0}, y_{0}\right)$, nhận $\vec{u}=(a ; b)$ là vecto chỉ phương, phương trình chính tắc của đường thẳng là $\frac{x-x_{0}}{a}=\frac{y-y_{0}}{b}$ với $(a, b \neq 0)$
PHƯƠNG PHÁP
Sử dụng định nghĩa
Bài toán: Cho hai điểm A(a, b), B(c, d). Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A và B.
Phương pháp:
Bước 1: Tính: $\overrightarrow{A B}=(c-a ; d-b)$ (vectơ chỉ phương của đường thẳng d)
Bước 2: Xác định vectơ pháp tuyến của đường thẳng d: $\vec{n}=(b-d ; c-a)$
Bước 3: Phương trình đường thẳng d:
$(b-d)(x-a)+(c-a)(y-b)=0$
Sử dụng phương trình tổng quát
Bài toán: Cho hai điểm A(a, b), B(c, d). Viết phương trình tổng quát của đường thẳng d đi qua hai điểm A và B.
Phương pháp:
Bước 1: Gọi phương trình tổng quát của đường thẳng d là y = mx + n (*)
Bước 2: Thay tọa độ A, B vào phương trình tổng quát ta thu được hệ phương trình ẩn m, n
$\left\{\begin{array}{l}b=a m+n \\ d=c m+n\end{array} \Rightarrow(m ; n)=(? ; ?)\right.$
Thay m, n vừa tìm được vào phương trình (*) ta suy ra phương trình cần tìm.
BÀI TẬP
Bài 1: Viết phương trình đường thẳng tham số, phương trình tổng quát đi qua 2 điểm A (1;2) và B (2;3). Vẽ đường thẳng vừa tìm được trên hệ tọa độ Oxy.
Hướng dẫn giải
| Cách 1: Sử dụng định nghĩa | Cách 2: Sử dụng phương trình tổng quát |
| $\overrightarrow{A B}=(1,1)$
Phương trình tham số: $\frac{x-1}{1}=\frac{y-2}{1}$ $\vec{n}=(-1,1)$ Phương trình tổng quát: $-1 .(x-1)+1 .(y-2)=0$ $\Rightarrow y=x+1$ |
$\overrightarrow{A B}=(1,1)$
Phương trình tham số: $\frac{x-1}{1}=\frac{y-2}{1}$ Gọi phương trình tổng quát là: y = ax + b Do PTĐT đi qua 2 điểm A, B nên ta có: Vậy PT tổng quát cần tìm là: $y=x+1$ |
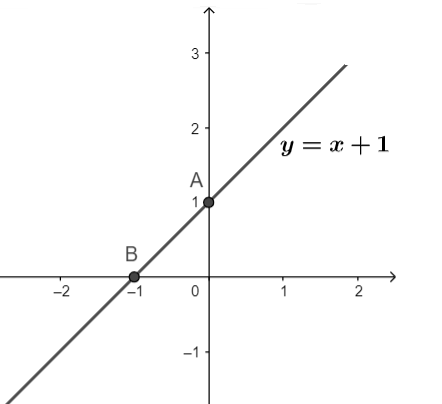
Bài 2: Viết phương trình đường thẳng y = ax + b biết
a) Đi qua 2 điểm A(-3,2), B (5,-4). Tính diện tích tam giác được tạo bởi đường thẳng và 2 trục tọa độ.
b) Đi qua A (3,1) song song với đường thẳng $y = -2x + m -1$
Hướng dẫn giải
a. Gọi phương trình tổng quát là: $y = ax + b$
Do PTĐT đi qua 2 điểm A, B nên ta có:
$\left\{\begin{array}{l}2=-3 a+b \\ -4=5 a+b\end{array} \Rightarrow(a ; b)=\left(-\frac{3}{4} ;-\frac{1}{4}\right)\right.$
Vậy PT tổng quát cần tìm là: $y=-\frac{3}{4} x-\frac{1}{4}$
Giao điểm của đường thẳng với trục Ox là: $y=0 \Rightarrow x=-\frac{1}{3} \Rightarrow A\left(-\frac{1}{3} ; 0\right)$
$\Rightarrow \overrightarrow{O A}=\left(-\frac{1}{3} ; 0\right) \Rightarrow|\overrightarrow{O A}|=\frac{1}{3}$
Giao điểm của đường thẳng với trục Oy là: $x=0 \Rightarrow y=-\frac{1}{4} \Rightarrow B\left(0 ;-\frac{1}{4}\right)$
$\Rightarrow \overrightarrow{O B}=\left(0 ;-\frac{1}{4}\right) \Rightarrow|\overrightarrow{O B}|=\frac{1}{4}$
$\Rightarrow S_{O A B}=\frac{1}{2} \cdot O A \cdot O B=\frac{1}{2} \cdot \frac{1}{3} \cdot \frac{1}{4}=\frac{1}{24}$
b. Gọi phương trình tổng quát là: y = ax + b
Do đường thẳng song song với y = -2x + m -1
⇒ a = -2
Phương trình đường thẳng trở thành y = -2x + b
Mà đường thẳng qua điểm A(3; 1)
⇒ 1 = 3.(-2) + b
⇒ b = 7
Vậy phương trình tổng quát là: y = -2x + 7

