PHƯƠNG PHÁP GIẢI
Để so sánh hai góc trong một tam giác ta làm như sau:
– Xét hai góc cần so sánh là hai góc của một tam giác.
– Tìm cạnh lớn hơn trong hai cạnh đối diện của hai góc ấy.
– Kết luận: Trong một tam giác góc đối diện với cạnh lớn hơn thì lớn hơn và ngược lại.
BÀI TẬP MINH HỌA
1A. So sánh các góc của tam giác ABC, biết rằng AB = 2 cm,
BC = 4 cm, AC = 5 cm.
1B. So sánh các góc của tam giác MNP, biết rằng MN = 8cm,
NP = 3 cm, MP = 10 cm.
2A. Cho tam giác ABC có AC > AB. So sanh hai góc ngoài tại các đỉnh B và C.
2B. Cho tam giác DEF có DE = 5 cm, DF = 7 cm. So sánh hai góc ngoài tại các đỉnh E và F.
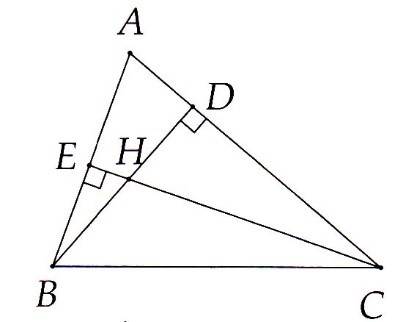
3A. Cho tam giác ABC có ba góc nhọn, AB < AC. Kẻ BD vuông góc với AC tại D, CE vuông góc với AB tại E. So sánh hai $ \displaystyle \widehat{{DBC}}$ và $ \displaystyle \widehat{{ECB}}$.
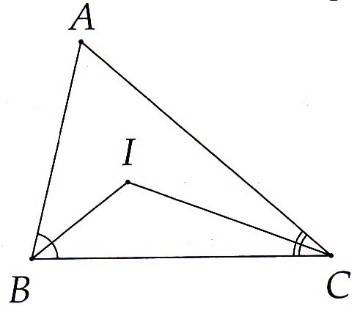
3B. Cho tam giác ABC có AB < AC. Tia phân giác của các góc B và C cắt nhau tại I. So sánh $ \displaystyle \widehat{{IBC}}$ và $ \displaystyle \widehat{{ICB}}$.
HƯỚNG DẪN GIẢI
1A. Ta có AB < BC < AC => $ \displaystyle \widehat{C}<\widehat{A}<\widehat{B}$
1B. Ta có NP < MN < MP => $ \displaystyle \widehat{M}<\widehat{P}<\widehat{N}$
2A. Ta có AC > AB => $ \displaystyle \widehat{B}>\widehat{C}$, do đó góc ngoài tại đỉnh B nhỏ hơn góc ngoài tại đỉnh C.
2B. Ta có DE < DE => $ \displaystyle \widehat{F}<\widehat{E}$, do đó góc ngoài tại đỉnh E nhỏ hơn góc ngoài tại đỉnh F.
3A. Vì AB < AC nên $ \displaystyle \widehat{{ACB}}<\widehat{{ABC}}$.
Lại có $ \displaystyle \widehat{{DBC}}=90{}^\circ -\widehat{{ABC}}$ và $ \displaystyle \widehat{{ECB}}=90{}^\circ -\widehat{{ABC}}$, từ đó ta có $ \displaystyle \widehat{{DBC}}>\widehat{{ECB}}$
3B. Vì AB < AC nên $ \displaystyle \widehat{{ACB}}<\widehat{{ABC}}$, với chú ý rằng $ \displaystyle \widehat{{IBC}}=\dfrac{{\widehat{{ABC}}}}{2},\widehat{{ICB}}=\dfrac{{\widehat{{ACB}}}}{2}$
Từ đó ta có $ \displaystyle \widehat{{IBC}}>\widehat{{ICB}}$