Muốn vẽ đồ thị hàm số bậc nhất y=ax+b chúng ta chỉ cần xác định 2 điểm phân biệt bất kì trên đường thẳng đó. Và nên chọn các điểm có tọa độ là số nguyên.
Trong chương trình Toán lớp 9 các em được học về hàm số bậc nhất có dạng $y=ax+b (a ≠ 0)$.
CÁCH VẼ LÝ THUYẾT
Thông thường để vẽ đồ thị hàm số bậc nhất $y=ax+b$ (kí hiệu là đường thẳng $d$) ta chọn 2 điểm như sau: $A(0 ; b)$ (là giao điểm của $d$ và $Oy$) và $B\left(-\dfrac{b}{a} ; 0\right)$ (là giao điểm của $d$ và $Ox$).
* Chú ý: Nếu tọa độ điểm B không nguyên thì nên chọn điểm khác.
VÍ DỤ VẼ ĐỒ THỊ HÀM SỐ Y=AX+B
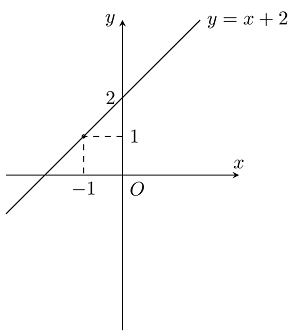
Ví dụ 1: Vẽ đồ thị hàm số $y=x+2$
Giải:
Ta có:
$x = 0$ ⇒ $y = 2$
$x = -1$ ⇒ $y = 1$
→ Đồ thị hàm số $y=x+2$ đi qua 2 điểm $(0;2)$ và $(-1;1)$.
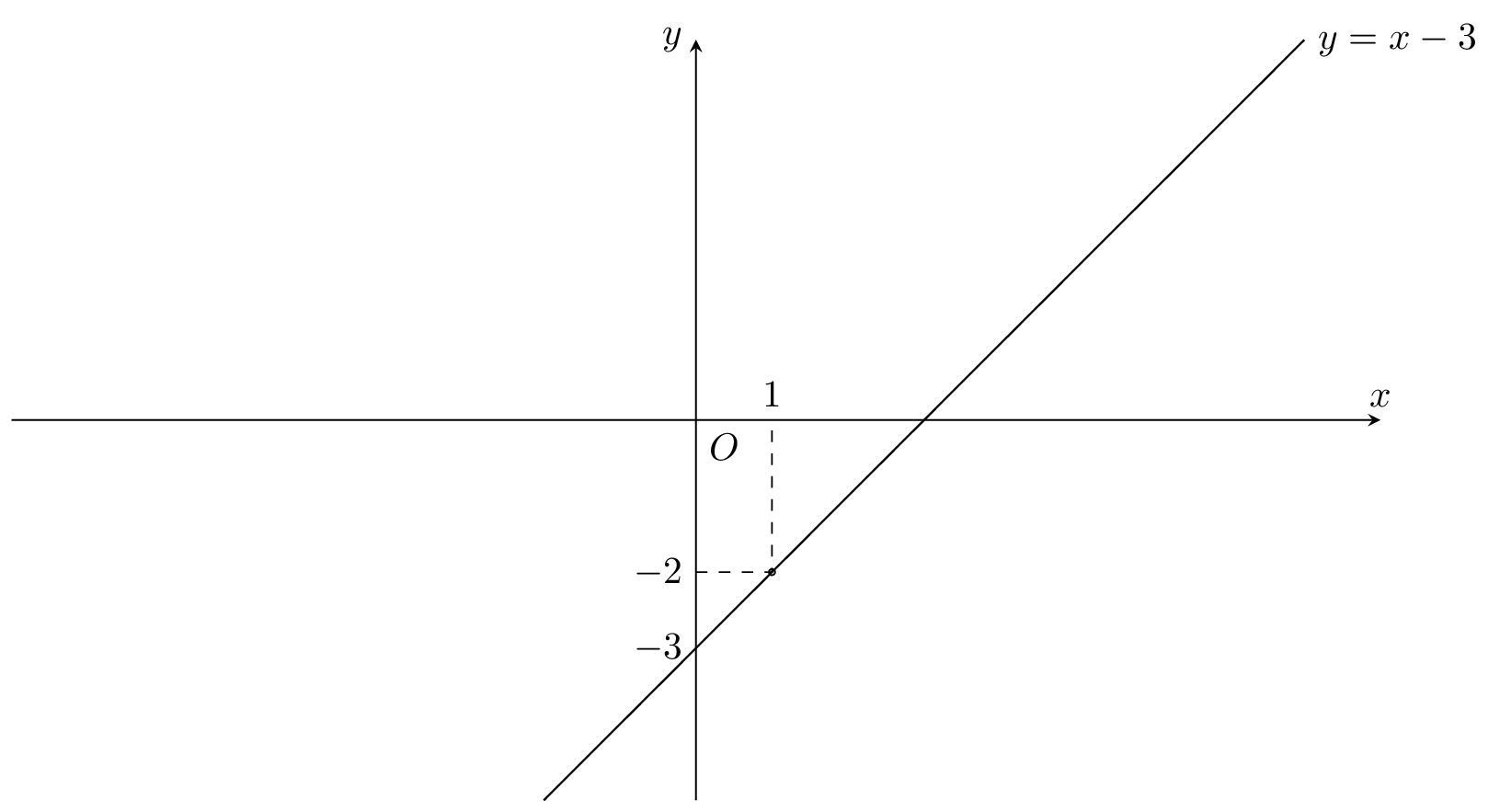
Ví dụ 2: Vẽ đồ thị hàm số $y=x-3$
Giải:
Ta có:
$x = 0$ ⇒ $y = -3$
$x = 3$ ⇒ $y = 0$
→ Đồ thị hàm số $y=x-3$ đi qua 2 điểm $(0;-3)$ và $(3;0)$.
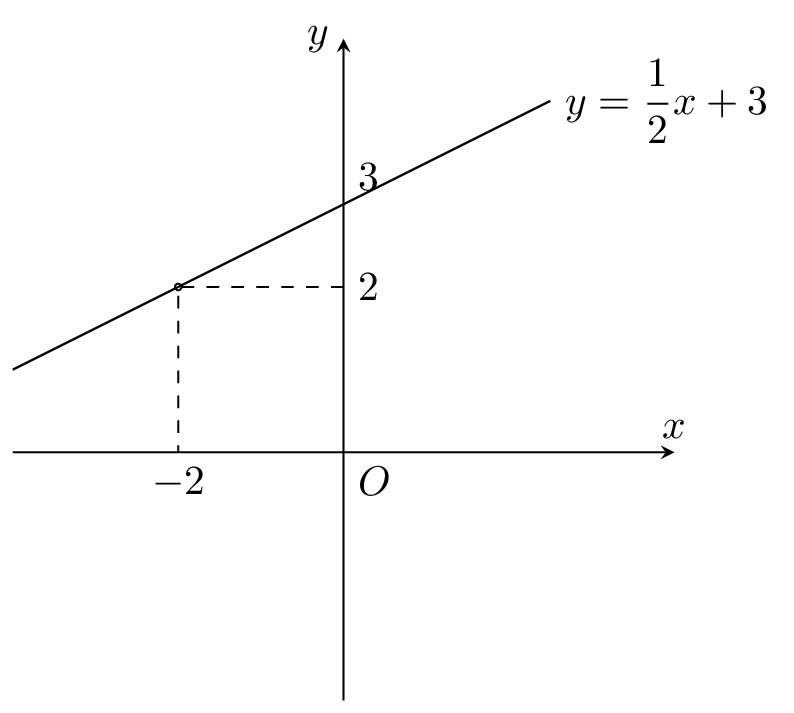
Ví dụ 3: Vẽ đồ thị hàm số $y=\dfrac{1}{2} x+3$
Giải:
Ta có:
$x = 0$ ⇒ $y = 3$
$x = -2$ ⇒ $y = 2$
→ Đồ thị hàm số $y=\dfrac{1}{2} x+3$ đi qua 2 điểm $(0;3)$ và $(-2;2)$.
BÀI TẬP VẼ ĐỒ THỊ HÀM SỐ Y=AX+B
Các em xem ví dụ ở trên để tập vẽ đồ thị hàm số hàm số bậc nhất $y=ax+b$ dưới đây:
a) $y = 1,5x + 2$
b) $y = 1,5x – 1$
c) $y= – 3x + 2$
d) $y=\dfrac{2}{3} x+3$
e) $y=\dfrac{-3}{2} x+2$
*Có khó khăn gì trong cách vẽ đồ thị hàm số $y=ax+b$ các em có thể comment bên dưới để được giải đáp.

