Bài tập vectơ – Hình học 10

I. PHÉP CỘNG – PHÉP TRỪ

1. Quy tắc ba điểm

Với ba điểm A, B, C tùy ý ta có:

+ $ \overrightarrow{{AB}}+\overrightarrow{{BC}}=\overrightarrow{{AC}};$

+ $ \overrightarrow{{AC}}-\overrightarrow{{AB}}=\overrightarrow{{BC}}.$

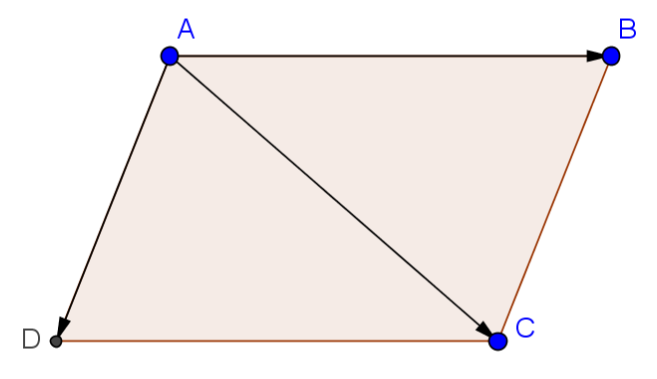
2. Quy tắc hình bình hành

Cho hình bình hành ABCD. Ta có $ \overrightarrow{{AB}}+\overrightarrow{{AD}}=\overrightarrow{{AC}}.$

3. Quy tắc trung điểm

Điểm I là trung điểm của đoạn thẳng $ AB\Leftrightarrow \overrightarrow{{IA}}+\overrightarrow{{IB}}=\overrightarrow{0}.$

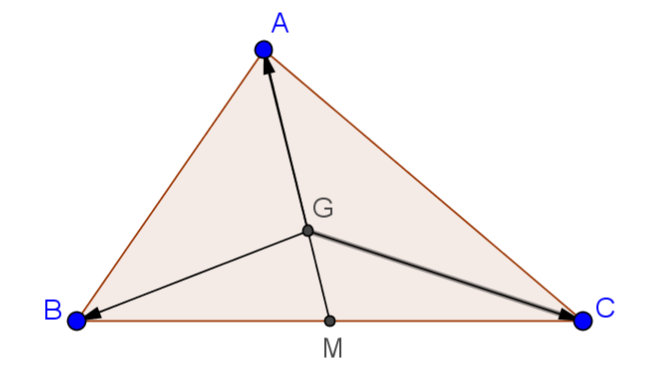
4. Quy tắc trọng tâm

Điểm G là trọng tâm của tam giác $ ABC\Leftrightarrow \overrightarrow{{GA}}+\overrightarrow{{GB}}+\overrightarrow{{GC}}=\overrightarrow{0}.$

II. BÀI TẬP

1. Cho hình bình hành ABCD. Hai điểm M, N lần lượt là trung điểm của BC và AD. Điểm I là giao điểm của AM và BN, K là giao điểm của DM và CN. Chứng minh $ \overrightarrow{{AM}}=\overrightarrow{{NC}},\overrightarrow{{DK}}=\overrightarrow{{NI}}.$

2. Cho tam giác ABC có H là trực tâm, O là tâm đường tròn ngoại tiếp. Gọi B’ là điểm đối xứng của B qua O. Chứng minh $ \overrightarrow{{AH}}=\overrightarrow{{B’C}}.$

3. Cho hình bình hành ABCD. Hai điểm M và N lần lượt là trung điểm của BC và AD.

a) Tìm tổng của hai vectơ $ \overrightarrow{{NC}}+\overrightarrow{{MC}};\overrightarrow{{AM}}+\overrightarrow{{CD}};\overrightarrow{{AD}}+\overrightarrow{{NC}}.$

b) Chứng minh $ \overrightarrow{{AM}}+\overrightarrow{{AN}}=\overrightarrow{{AB}}+\overrightarrow{{AD}}.$

4. Cho tam giác ABC. Các điểm M, N và P lần lượt là trung điểm của AB, AC và BC. Tìm hiệu của các vectơ $ \overrightarrow{{AM}}-\overrightarrow{{AN}},\overrightarrow{{MN}}-\overrightarrow{{NC}},\overrightarrow{{MN}}-\overrightarrow{{PN}},\overrightarrow{{BP}}-\overrightarrow{{CP}}.$

5. Cho hình thoi ABCD có cạnh a, tâm O và $ \widehat{{BAD}}=60^{\circ }.$ Tính $ \displaystyle \left| {\overrightarrow{{AB}}+\overrightarrow{{AD}}} \right|,\left| {\overrightarrow{{BA}}-\overrightarrow{{BC}}} \right|,\left| {\overrightarrow{{OB}}-\overrightarrow{{DC}}} \right|.$

6. Cho hình vuông ABCD có cạnh a, tâm O. Tính $ \displaystyle \left| {\overrightarrow{{OA}}-\overrightarrow{{CB}}} \right|,\left| {\overrightarrow{{AB}}+\overrightarrow{{DC}}} \right|,\left| {\overrightarrow{{CD}}-\overrightarrow{{DA}}} \right|.$

7. Chứng minh rằng $ \left| {\overrightarrow{a}+\overrightarrow{b}} \right|\le \left| {\overrightarrow{a}} \right|+\left| {\overrightarrow{b}} \right|.$ Khi nào xẩy ra dấu đẳng thức?

8. Cho sáu điểm A, B, C, D, E và F. Chứng minh rằng $ \overrightarrow{{AD}}+\overrightarrow{{BE}}+\overrightarrow{{CF}}=\overrightarrow{{AE}}+\overrightarrow{{BF}}+\overrightarrow{{CD}}.$

9. Gọi O là tâm của tam giác đều ABC. Chứng minh rằng $ \overrightarrow{{OA}}+\overrightarrow{{OB}}+\overrightarrow{{OC}}=\overrightarrow{0}.$

10. Cho hình bình hành ABCD tâm O. Chứng minh rằng:

a) $ \overrightarrow{{AB}}+\overrightarrow{{BC}}+\overrightarrow{{CD}}+\overrightarrow{{DA}}=\overrightarrow{0}.$
b) $ \overrightarrow{{AB}}-\overrightarrow{{CD}}=\overrightarrow{{AC}}-\overrightarrow{{BD}}.$
c) $ \overrightarrow{{OA}}+\overrightarrow{{OB}}+\overrightarrow{{OC}}+\overrightarrow{{OD}}=\overrightarrow{0}.$

11. Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho $ AE=EF=FC.$ BE cắt AM tại N. Chứng minh $ \overrightarrow{{NA}}$ và $ \overrightarrow{{NM}}$ là hai vectơ đối nhau.

12. Cho hai điểm phân biệt A và B. Tìm điểm M thỏa mãn một trong các điều kiện sau:

a) $ \overrightarrow{{MA}}-\overrightarrow{{MB}}=\overrightarrow{{BA}};$ b) $ \overrightarrow{{MA}}-\overrightarrow{{MB}}=\overrightarrow{{AB}};$ c) $ \overrightarrow{{MA}}+\overrightarrow{{MB}}=\overrightarrow{0}.$

13. Cho tam giác ABC. Chứng minh rằng nếu $ \left| {\overrightarrow{{CA}}+\overrightarrow{{CB}}} \right|=\left| {\overrightarrow{{CA}}-\overrightarrow{{CB}}} \right|$ thì tam giác ABC vuông tại C.

14. Cho ba điểm O, A, B không thẳng hàng. Với điều kiện nào thì vectơ $ \overrightarrow{{OA}}+\overrightarrow{{OB}}$ nằm trên đường phân giác của góc $ \widehat{{BOA}}?$

15. Cho hình bình hành ABCD. Gọi O là một điểm bất kì trên đường chéo AC. Qua O kẻ các đường thẳng song song với các cạnh của hình bình hành. Các đường thẳng này cắt AB và DC lần lượt tại M và N, cắt AD và BC lần lượt tại E và F. Chứng minh rằng:

a) $ \overrightarrow{{OA}}+\overrightarrow{{OC}}=\overrightarrow{{OB}}+\overrightarrow{{OD}};$

b) $ \displaystyle \overrightarrow{{BD}}=\overrightarrow{{ME}}+\overrightarrow{{FN}}.$

*Download file Bài tập vectơ – Hình học 10.docx bằng cách click vào nút Tải về dưới đây.