KIẾN THỨC CẦN NHỚ
1. Hình thoi
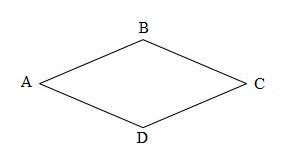
Hình thoi ABCD có:
– Cạnh AB song song với cạnh DC
– Cạnh AD song song với cạnh BC
– $A B=B C=C D=A D$
Hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
2. Diện tích hình thoi
Cho hình thoi ABCD có $A C=m, B D=n$.
Cắt hình tam giác AOD và hình tam giác COD rồi ghép với hình tam giác ABC để được hình chữ nhật MNCA (xem hình vẽ).
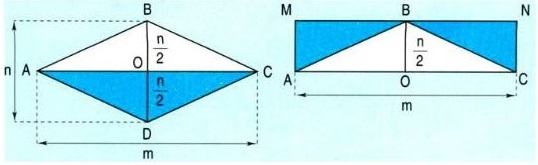
Dựa theo hình vẽ ta có:
Diện tích hình thoi ABCD bằng diện tích hình chữ nhật MNCA.
Diện tích hình chữ nhật MNCA là $\displaystyle m \times \frac{n}{2}$. Mà $\displaystyle m \times \frac{n}{2}=\frac{m \times n}{2}$.
Vậy diện tích hình thoi ABCD là $\displaystyle\frac{m \times n}{2}$.
Diện tích hình thoi bằng tích độ dài hai đường chéo chia cho 2 (cùng một đơn vị đo)
$\displaystyle S=\frac{m \times n}{2}$
(S là diện tích của hình thoi; m, n là độ dài của hai đường chéo).
CÁC DẠNG TOÁN
Dạng 1: Tính diện tích hình thoi khi biết độ dài hai đường chéo
Phương pháp: Áp dụng công thức:$\displaystyle S=\frac{m \times n}{2}$ (S là diện tích hình thoi; m, n là độ dài hai đường chéo)
Dạng 2: Tính độ dài đường chéo khi biết diện tích và độ dài đường chéo còn lại
Phương pháp: Từ công thức tính diện tích $\displaystyle S=\frac{m \times n}{2}$, ta có công thức tính độ dài một đường chéo như sau: $m=S \times 2\colon n$ hoặc $n=S \times 2\colon m$.
Dạng 3: Toán có lời văn
Phương pháp: Đọc kĩ đề bài, xác định toán trong bài rồi giải bài toán.
BÀI TẬP VÍ DỤ
Ví dụ 1: Diện tích hình thoi có độ dài đường chéo là $17 cm$ và $8 cm$ là:
Bài giải:
Diện tích hình thoi đó là:
$\displaystyle\frac{17 \times 8}{2}=68\left(\mathrm{~cm}^{2}\right)$
Đáp số: $68 cm^{2}$
Ví dụ 2: Một hình thoi có diện tích là $224 cm^{2}$ và đường chéo lớn là $28 cm$. Vậy độ dài đường chéo bé là:
Bài giải:
Độ dài đường chéo bé của hình thoi là:
$224 \times 2\colon 28=16 cm $
Đáp số: $16 cm$.

