Phiếu bài tập Toán lớp 9 – Tuần 31

Phiếu bài tập cuối tuần môn Toán lớp 9 – Tuần 31: Phương trình quy về phương trình bậc hai. Hình nón, hình nón cụt.

Bài 1: Giải phương trình

a) $\dfrac {x+3}{4}-3=\dfrac {( x+5 )( x-2 )}{3}$

b) $\dfrac {14}{x^2-9}+\dfrac {4-x}{x+3}=\dfrac {7}{x+3}-\dfrac {1}{3-x}$

c) $\dfrac {\left( x+5 \right)^2}{2}-\dfrac {x}{3}=\dfrac {\left( x-3 \right)^2}{3}$

d) $\dfrac {2}{x^2-4}-\dfrac {1}{x\left( x-2 \right)}+\dfrac {x-4}{x\left( x+2 \right)}=0$

Bài 2: Giải các phương trình trùng phương:

a) $ x^4-25x^2+144=0$

b) $ x^4-6x^2-7=0$

c) $3x^4-11x^2-4=0$

d) $4x^2-29+\dfrac {25}{x^2}=0$

Bài 3: Giải các phương trình sau bằng cách đưa về dạng tích:

a) $ x( x-1 )( x-2 )-x^3+1=0$

b) $4x^3+6x^2-2x-3=0$

c) $ x^3-3x^2-3x+1=0$

d) $( 2x^2-5x+1 )^2=( x^2-5x+6 )^2$

Bài 4: Giải phương trình: $ x^2-| 3x-2 |=0$

Bài 5: Cho phương trình $ x^4-( 3m+14 )x^2+( 4m+12 )( 2-m )=0$

a) Tìm điều kiện của m để phương trình có 4 nghiệm phân biệt

b) Xác định m sao cho tích của 4 nghiệm đó lớn nhất.

Bài 6: Một miếng bìa có dạng nửa hình tròn tâm O bán kính $R=2\sqrt {3}dm$ được cuốn lại thành hình nón đỉnh O với đường sinh bằng R. Tính diện tích toàn phần và thể tích của hình nón.

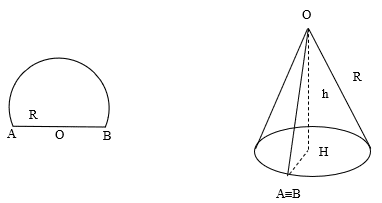
Bài 7: Cho tam giác ABC vuông tại A, AB =4cm, AC =3cm. Quay tam giác vuông ABC một vòng quanh cạnh AB, ta được một hình nón có diện tích xung quanh S₁, thể tích V₁. Quay tam giác vuông đó một vòng quanh cạnh AC, ta được một hình nón có diện tích xung quanh S₂, thể tích V₂.

a) Tính tỉ số S₁: S₂

b) Tính tỉ số V₁ :V₂

Bài 8: Một hình nón cụt có chiều cao bằng 12cm, các bán kính đáy bằng 15cm và 20cm.

a) Tính diện tích xung quanh của hình nón cụt.

b) Tính thể tích của hình nón cụt.

Bài 9: Một chi tiết máy có dạng và kích thước như hình.

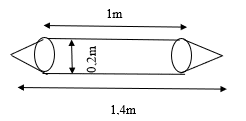
Tính (làm tròn kết quả đến chữ số thập phân thứ ba).

a) Diện tích bề mặt của chi tiết máy

b) Thể tích của chi tiết máy đó.

Bài 10: Tính thể tích của một cái thùng có hình dạng và kích thước được biểu diễn trong hình sau (làm tròn kết quả đến chữ số thập phân thứ ba).

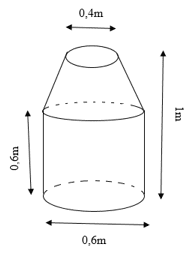
* Download file word: PHIẾU BÀI TẬP TOÁN LỚP 9 – TUẦN 31.docx bằng cách click vào nút Tải về dưới đây: