1. Hàm số $y=\sin x$
Có TXĐ $D=R$, là hàm số lẻ, tuần hoàn với chu kì $2 \pi$, nhận mọi giá trị thuộc đoạn $[-1 ; 1]$.
– Đồng biến trên mỗi khoảng $\displaystyle\left(-\frac{\pi}{2}+k 2 \pi ; \frac{\pi}{2}+k 2 \pi\right)$ và nghịch biến trên mỗi khoảng $\displaystyle\left(\frac{\pi}{2}+k 2 \pi ; \frac{3 \pi}{2}+k 2 \pi\right)$
Có đồ thị đi qua điểm $O(0 ; 0)$
2. Hàm số $y=\cos x$
– Có TXĐ $D=R$, là hàm số chẵn, tuần hoàn với chu kì $2 \pi$, nhận mọi giá trị thuộc đoạn $[-1 ; 1]$.
– Đồng biến trên mỗi khoảng $\displaystyle (-\pi+k 2 \pi ; k 2 \pi)$ và nghịch biến trên mỗi khoảng $\displaystyle (k 2 \pi ; \pi+k 2 \pi)$
– Có đồ thị đi qua điểm $(0 ; 1)$

Đồ thị hàm số sin và cosin
3. Hàm số $y=\tan x$
Có TXĐ $\displaystyle D=R \backslash\left\{\frac{\pi}{2}+k \pi, k \in Z\right\}$, là hàm số lẻ, tuần hoàn với chu kì $\pi$, nhận mọi giá trị thuộc $R$.
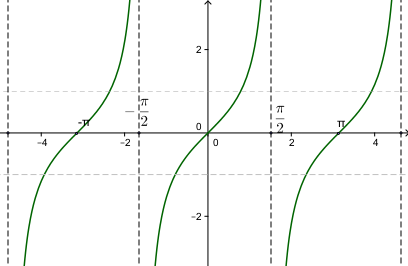
Đồ thị hàm số tan
Đồng biến trên mỗi khoảng $\displaystyle\left(-\frac{\pi}{2}+k \pi ; \frac{\pi}{2}+k \pi\right)$.
4. Hàm số $y=\cot x$
– Có TXĐ $\displaystyle D=R \backslash\{k \pi, k \in Z\}$, là hàm số lẻ, tuần hoàn với chu kì $\pi$, nhận mọi giá trị thuộc $R$.
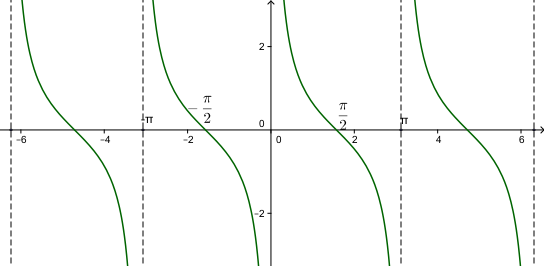
Đồ thị hàm số cot
– Nghịch biến trên mỗi khoảng $\displaystyle (k \pi ; \pi+k \pi)$.

