A. LÝ THUYẾT TAM GIÁC ĐỒNG DẠNG
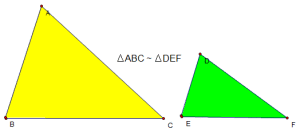
1. Trường hợp đồng thứ nhất: cạnh – cạnh – cạnh (c – c – c)
Xét ∆ABC và ∆DEF, ta có :
$\dfrac{A B}{D E}=\dfrac{A C}{D F}=\dfrac{B C}{E F}$
⇒ ∆ABC ~ ∆DEF (c – c – c)
2. Trường hợp đồng dạng thứ 2: cạnh – góc – cạnh (c – g – c)
2 cạnh tương ứng tỉ lệ với nhau – góc xen giữa hai cạnh bằng nhau (c – g – c)
Xét ∆ABC và ∆DEF, ta có :
$\dfrac{A B}{D E}=\dfrac{A C}{D F}$
$\widehat{A}=\widehat{D}$
⇒ ∆ABC ~ ∆DEF (c – g – c)
3. Trường hợp đồng dạng 3: góc – góc (g – g)
2 góc tương ứng bằng nhau
Xét ∆ABC và ∆DEF, ta có :
$\widehat{A}=\widehat{D}$
$\widehat{B}=\widehat{E}$
⇒ ∆ABC ~ ∆DEF (g – g)
4. Các trường hợp đồng dạng của tam giác vuông
a. Trường hợp 1: cạnh huyền – cạnh góc vuông
Nếu cạnh huyền và cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác đồng dạng.
b. Trường hợp 2: hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia thì hai tam giác đồng dạng.
c. Trường hợp 3: góc nhọn
Nếu góc nhọn của tam giác này bằng góc nhọn của tam giác kia thì hai tam giác đồng dạng.
B. BÀI TẬP CÓ LỜI GIẢI
Dưới đây là một số bài tập chứng minh 2 tam giác đồng dạng có lời giải để các em học sinh học cách giải.
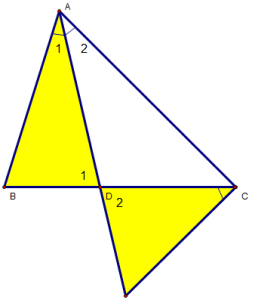
Bài 1: Cho ∆ABC (AB < AC), có AD là đường phân giác trong. Ở miền ngoài ∆ABC vẽ tia Cx sao cho $\widehat{B C x}=\widehat{B A D}$. Gọi I là giao điểm của Cx và AD. Chứng minh rằng:
a) ∆ADB đồng dạng ∆CDI.
b) $\dfrac{A D}{A C}=\dfrac{A B}{A I}$
c) AD2 = AC – BD.DC
Giải:
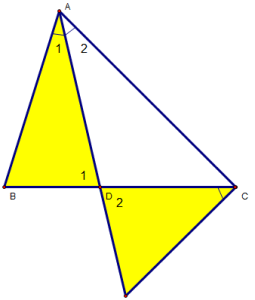
a)∆ADB và ∆CDI , ta có:
$\widehat{B C x}=\widehat{B A D}$(gt)
$\widehat{D_{1}}=\widehat{D_{2}}$(đối đỉnh)
⇒ ∆ADB ~ ∆CDI
b) )∆ABD và ∆AIC , ta có :
$\widehat{B}=\widehat{I}$(∆ADB ~ ∆CDI)
$\widehat{A_{1}}=\widehat{A_{2}}$(AD là phân giác)
⇒ ∆ABD ~ ∆AIC
⇒$\dfrac{A D}{A C}=\dfrac{A B}{A I}$
c)
⇒ AD.AI = AB.AC (1)
mà: $\dfrac{A D}{C D}=\dfrac{BD}{D I}$(∆ADB ~ ∆CDI )
⇒ AD.DI = BD.CD (2)
từ (1) và (2) :
AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI ) = AD.AD = AD2
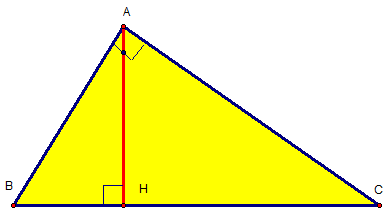
Bài 2: Cho tam giác ABC vuông tại A, có đường cao AH . Chứng minh các hệ thức :
a) AB2 = BH.BC và AC2 = CH.BC
b) AB2 +AC2 = BC2
c) AH2 = BH.CH
d) AH.BC = AB.AC
Giải:
a) Xét hai ∆ABC và ∆ HAC, ta có: AC2 = CH.BC :
$\widehat{B A C}=\widehat{A H C}=90^{\circ}$
$\widehat{C}$ là góc chung.
⇒ ∆ABC ~ ∆HAC (g – g)
⇒ $\dfrac{A C}{H C}=\dfrac{B C}{A C}$
⇒ AC2 = CH.BC (1)
Chứng minh tương tự: AB2 = BH.BC (2)
b) AB2 +AC2 = BC2
Từ (1) và (2), ta có :
AB2 +AC2 = BH.BC + CH.BC = (BH + CH)BC = BC2
c) AH2 = BH.CH :
Xét hai ∆HBA và ∆ HAC, ta có :
$\widehat{B H C}=\widehat{A H C}=90^{0}$
$\widehat{A B H}=\widehat{H A C}$ cùng phụ $\widehat{B A H}$
⇒ ∆HBA ~ ∆HAC (g – g)
⇒ $\dfrac{H A}{H C}=\dfrac{H B}{H A}$
⇒ AH2 = BH.CH
AH.BC = AB.AC :
Ta có: $\dfrac{H A}{A B}=\dfrac{A C}{B C}$ (∆ABC ~ ∆HAC)
⇒ AH.BC = AB.AC
Bài 3: Cho ∆ABC nhọn. kẻ đường cao BD và CE. vẽ các đường cao DF và EG của ∆ADE. Chứng minh:
a) ∆ABD đồng dạng ∆AEG.
b) AE = AB.AG = AC.AF
c) FG // BC
Giải:
a) xét ∆ABD và ∆AEG, ta có :
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
⇒ BD // EG
⇒ ∆ABD ~ ∆AGE
b) ⇒ $\dfrac{A B}{A E}=\dfrac{A D}{A G}$
⇒ AD.AE = AB.AG (1)
Chứng minh tương tự, ta được : AD.AE = AC.AF (2)
từ (1) và (2) suy ra :
AD.AE = AB.AG = AC.AF
c) xét ∆ABC, ta có :
AB.AG = AC.AF (cmt)
$\dfrac{A B}{A F}=\dfrac{A C}{A G}$
⇒ FG // BC (định lí đảo talet)

