Phiếu bài tập cuối tuần môn Toán lớp 8 – Tuần 4: Những hằng đẳng thức đáng nhớ (tiếp). Luyện tập hình.
Bài 1: Rút gọn các biểu thức sau:
a) $( a^2-1 )^3-( a^4+a^2+1 )( a^2-1 );$
b) $( a^4-3a^2+9 )( a^2+3 )-( 3+a^2 )^3 $
Bài 2: Tính giá trị của các biểu thức sau:
a) $A=2( m^3+n^3 )-3( m^2+n^2 ),$ với m + n = 1;
b) $B=2m^6+3m^3n^3+n^6+n^3,$ với $ m^3+n^3=1 $
c) $C=( a-1 )^3-4a( a+1 )( a-1 )+3( a-1 )( a^2+a+1 )$, với a = -3;
d) $D=( y-1 )( y-2 )( 1+y+y^2 )( 4+2y+y^2 )$, với y = 1.
Bài 3: Cho a + b + c = 0. Chứng minh rằng: $ a^3+b^3+c^3=3abc $
Bài 4: Chứng minh rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến: ..
Bài 5: Tính:
$ a)~A=\dfrac {37^3+12^3}{49}-37\cdot 12$ $ b)~B=\dfrac {52^3-48^3}{4}+52\cdot 48 $.
Bài 6: Trên hình vẽ 6. Tính góc C
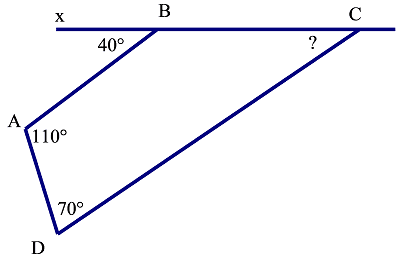
Bài 7:
a) Cho tam giác ABC, M là trung điểm của BC, D trên AC sao cho $CD=2AD$. AM cắt BD tại I. Chứng minh I là trung điểm của AM.
b) Cho tam giác ABC có trung tuyến AM. Gọi I là trung điểm của AM, BI cắt AC tại. Chứng minh $AD=\dfrac {1}{2}DC$
Bài 8: Cho tam giác ABC có trung tuyến BD và CE. Gọi M , N thứ tự là trung điểm của BE và CD. MN cắt BD và CE thứ tự tại I và K.
a) Tính độ dài MN
b) Chứng minh $MI=IK=KN$
Bài 9: Cho tam giác ABC. Trên cạnh AB lấy $AD=DE=EB$. Từ D, E kẻ các đường thẳng cùng song song với BC cắt AC lần lượt tại M, N. Chứng minh:
a) M là trung điểm của AN
b) $AM=MN=NC$
c) $2EN=DM+BC$
d) $S_{ABC}=3S_{AMB}$
Bài 10: Cho tam giác ABC nhọn, trực tâm H, trung điểm M của BC. Qua H kẻ đường vuông góc với HM, cắ AB và AC tại E và F. Trên tia đối của HC lấy HD= HC. Chứng minh:
a) HM//BD
b) E là trực tâm tam giác DHB
c) DE//AC
d) HE=HF
* Download file word: PHIẾU BÀI TẬP TOÁN LỚP 8 – TUẦN 4.docx bằng cách click vào nút Tải về dưới đây:

