Hướng dẫn học sinh giải bài tập sách giáo khoa toán lớp 9 tập 1 trang 6, 7. Bài học Căn thức bậc hai.
Bài 1. (Trang 6 SGK Toán 9 – Tập 1)
Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng:
121, 144, 169, 225, 256, 324, 361, 400
Bài giải
Ta có căn bậc hai của $121$ là:
$\displaystyle\sqrt{121}=11$ vì $11>0$ và $11^{2}=121$.
Tương tự:
$\displaystyle\sqrt{144}=12$; $\displaystyle\sqrt{169}=13$; $\displaystyle\sqrt{225}=15$;
$\displaystyle\sqrt{256}=16$; $\displaystyle\sqrt{324}=18$; $\displaystyle\sqrt{361}=19$;
$\displaystyle\sqrt{400}=20$.
Bài 2. (Trang 6 SGK Toán 9 – Tập 1)
So sánh:
a) $2$và $\displaystyle\sqrt{3}$;
b) $6$và $\displaystyle\sqrt{41}$;
c) $7$và $\displaystyle\sqrt{47}$.
Bài giải
a) $\displaystyle\left.\begin{array}{l}2=\sqrt{4} \\ \sqrt{3}\end{array}\right\}$ vì $4>3$$\displaystyle\Rightarrow \sqrt{4}>\sqrt{3} \Rightarrow 2>\sqrt{3}$.
b) $\displaystyle\left.\begin{array}{l}6=\sqrt{36} \\ \sqrt{41}\end{array}\right\}$ vì $41>36$ $\displaystyle\Rightarrow \sqrt{41}>\sqrt{36} \Rightarrow \sqrt{41}>6$.
c) $\displaystyle\left.\begin{array}{l}7=\sqrt{49} \\ \sqrt{47}\end{array}\right\}$ vì $\displaystyle\sqrt{49}>\sqrt{47} \Rightarrow 7>\sqrt{47}$.
Bài 3. (Trang 6 SGK Toán 9 – Tập 1)
Dùng máy tính bỏ túi, tính giá trị gần đúng của mỗi nghiệm phương trình sau (làm tròn đến chữ số thập phân thứ ba):
a) $x^{2}=2$;
b) $x^{2}=3$;
c) $x^{2}=3,5$;
d) $x^{2}=4,12$.
Bài giải
Hướng dẫn: nghiệm của phương trình $x^{2}=a$ ( với $a \geq 0$) là các căn bậc hai của a.
Bài 4. (Trang 7 SGK Toán 9 – Tập 1)
Tìm số $x$ không âm, biết:
a) $\displaystyle\sqrt{x}=15$;
b) $\displaystyle 2 \sqrt{x}=14$;
c) $\displaystyle\sqrt{x}<\sqrt{2}$;
d) $\displaystyle\sqrt{2 x}<4$.
Bài giải
a) $\displaystyle\sqrt{x}=15 \Leftrightarrow(\sqrt{x})^{2}=15^{2} \Leftrightarrow x=225 \cdot $
b) $\displaystyle 2 \sqrt{x}=14 \Leftrightarrow \sqrt{x}=7 \Leftrightarrow(\sqrt{x})^{2}=7^{2} \Leftrightarrow x=49 \cdot $
c) $\displaystyle\sqrt{x}<\sqrt{2} \Leftrightarrow(\sqrt{x})^{2}<(\sqrt{2})^{2} \Leftrightarrow 0 \leq x<2$.
d) $\displaystyle\sqrt{2 x}<\sqrt{4} \Leftrightarrow(\sqrt{2 x})^{2}<4^{2} \Leftrightarrow 0 \leq 2 x<16 \Leftrightarrow 0 \leq x<8$.
Bài 5. (Trang 7 SGK Toán 9 – Tập 1)
Tính cạnh một hình vuông, biết diện tích của nó bằng diện tích của hình chữ nhật có chiều rộng 3,5m và chiều dài 14m.
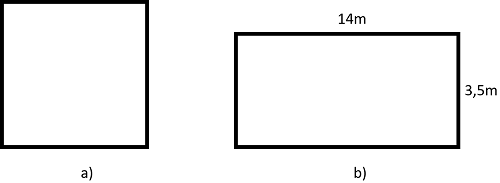
Bài giải
Diện tích của hình chữ nhật bằng:
$3,5 m \times 14 m=49\left(m^{2}\right)$.
Vì diện tích hình chữ nhật bằng diện tích hình vuông nên cạnh hình vuông bằng $\displaystyle\sqrt{49}=7(m)$.

