PHƯƠNG PHÁP GIẢI
Để chứng minh một tia là tia phân giác của một góc, ta có thể sử dụng các cách sau:
– Cách 1: Áp dụng Định lí đảo.
Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
– Cách 2: Chứng minh hai góc bằng nhau dựa vào hai tam giác bằng nhau.
– Cách 3: Đường trung tuyến trong tam giác cân đồng thời là đường phân giác.
BÀI TẬP MINH HỌA
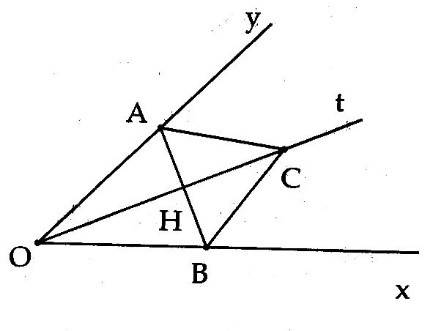
4A. Cho $ \displaystyle \widehat{{xOy}}$ có tia phân giác Ot. Trên tia Ot lấy điểm C bất kì. Lấy
A $ \displaystyle \in $ Ox, B $ \displaystyle \in $ Oy sao cho OA = OB. Gọi H là giao điểm của AB và Ot. Chứng minh:
a) CA = CB và CO là phân giác của $ \displaystyle \widehat{{ACB}}$;
b) OC vuông góc với AB tại trung điểm của AB;
c) Biết AB = 6 cm, OA = 5 cm. Tính OH
4B. Cho $ \displaystyle \Delta $ABC, AB = AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh:
a) BE = CD;
b) $ \displaystyle \Delta $BMD = $ \displaystyle \Delta $CME;
c) Đường vuông góc với OE tại E cắt Ox, Oy lần lượt tại M, N. Chứng minh MN / / AC //BD.
5A. Cho $ \displaystyle \widehat{{xOy}}$. Lấy các điểm A,B thuộc tia Ox sao cho OA > OB. Lấy các điểm C, D thuộc Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh.:
a) AD = BC ;
b) $ \displaystyle \Delta $ABE = $ \displaystyle \Delta $CDE;
c) OE là tia phân giác của góc xOy.
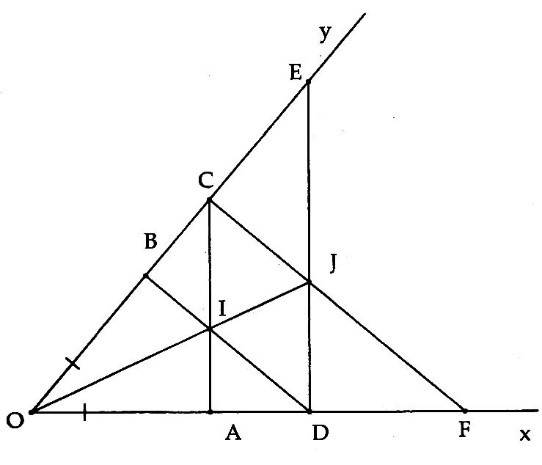
5B. Cho góc nhọn xOy. Trên cạnh Ox lấy điểm A và trên cạnh Oy lấy điểm B sao cho OA = OB. Đường vuông góc với Ox kẻ từ A cắt Oy tại điểm C. Đường vuông góc với Oy kẻ từ B cắt Ox tại D và cắt AC tại I. Đường vuông góc với Ox kẻ qua D cắt Oy tại E. Đường vuông góc với Oy kẻ qua C cắt Ox tại F và cắt DE tại J.
a) Chứng minh OI là tia phân giác $ \displaystyle \widehat{{xOy}}$.
b) Chứng minh OC = OD. Từ đó suy ra OJ là tia phân giác của $ \displaystyle \widehat{{xOy}}$
c) Chứng minh ba điểm O, I, J thẳng hàng.
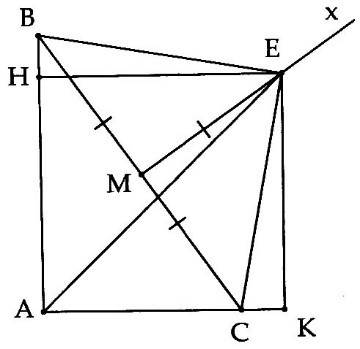
6A. Cho $ \displaystyle \Delta $ABC vuông tại A. Gọi M là trung điểm của BC. Trên nửa mặt phẳng bờ BC không chứa A dựng tia Mx $ \displaystyle \bot $ BC. Trên tia Mx lấy E sao cho ME = MB.
a) Tam giác BEC là tam giác gì?
b) Gọi H và K là chân các đường vuông góc kẻ từ E đến các đường thẳng AB, AC. Chứng minh $ \displaystyle \widehat{{BEH}}=\widehat{{CEK}}$.
c) Chứng minh rằng AE là tia phân giác của góc A
6B. Cho $ \displaystyle \Delta $ABC vuông tại A. Trên nửa mặt phẳng bờ BC không chứa A dựng $ \displaystyle \Delta $BCD vuông cân tại D. Hạ DI $ \displaystyle \bot $AB, DH $ \displaystyle \bot $AC.
Chứng minh AD là tia phân giác của $ \displaystyle \widehat{A}$
HƯỚNG DẪN GIẢI
4A. a) Vì Ot là phân giác $ \displaystyle \widehat{{xOy}}$ nên $ \displaystyle \widehat{{AOC}}=\widehat{{BOC}}$
=> $ \displaystyle \Delta $AOC = $ \displaystyle \Delta $BOC (c.g.c) => CA = CB, $ \displaystyle \widehat{{OCA}}=\widehat{{OCB}}$
=> CO là phân giác $ \displaystyle \widehat{{ACB}}$.
b) Chúng minh được: $ \displaystyle \Delta $OAH = $ \displaystyle \Delta $OBH (c.g.c).
=> $ \displaystyle \widehat{{OAH}}=\widehat{{OHB}}$ = 90°, AH = BH.
Vậy OC vuông góc với AB tại trung điểm của AB.
c) Vì H là trung điểm của AB
=> AH = $ \displaystyle \dfrac{1}{2}$ AB = 3 cm.
Áp dụng định lí Pytago trong tam giác vuông OHA, tính được OH = 4 cm.
4B. a) $ \displaystyle \Delta $ABE = $ \displaystyle \Delta $ACD (c.g.c) => BE = CD.
b) Do $ \displaystyle \Delta $ABE = $ \displaystyle \Delta $ACD => $ \displaystyle \widehat{{ABE}}=\widehat{{ACD}}=>\widehat{{BDC}}=\widehat{{CEB}}$.
Mặt khác AB = AC, AD = AE => BD = CE.
Lại có: $ \displaystyle \Delta $ABE = $ \displaystyle \Delta $ACD => $ \displaystyle \widehat{{ABE}}=\widehat{{ACD}}=>\widehat{{DBM}}=\widehat{{ECM}}$
=> $ \displaystyle \Delta $BMD = $ \displaystyle \Delta $CME (g.c.g).
c) Vì $ \displaystyle \Delta $BMD = $ \displaystyle \Delta $CME => MD = ME => $ \displaystyle \Delta $ADM = $ \displaystyle \Delta $AEM(c.c.c).
=> $ \displaystyle \widehat{{MAD}}=\widehat{{MAE}}$ => AM là phân giác của $ \displaystyle \widehat{{BAC}}$.
5A. a) $ \displaystyle \Delta $OAD = $ \displaystyle \Delta $OCB (c.g.c) => AD = CB.
b) Do OA = OC, OB = OD => AB = CD.
Lại có $ \displaystyle \Delta $OAD = $ \displaystyle \Delta $OCB (c.g.c) => $ \displaystyle \widehat{{OBC}}=\widehat{{ODA}}=>\widehat{{ABE}}=\widehat{{CDE}}$
Mà $ \displaystyle \widehat{{OAD}}=\widehat{{OCB}}$. Vậy $ \displaystyle \Delta $ABE = $ \displaystyle \Delta $CDE (g.c.g)
c) Vì $ \displaystyle \Delta $ABE = $ \displaystyle \Delta $CDE (g.c. g) => $ \displaystyle \widehat{{BOE}}=\widehat{{DOE}}$
=> OE là tia phân giác của góc xOy.
Tam giác AOC và BOD đều cân ở O nên OE $ \displaystyle \bot $ BD và OE $ \displaystyle \bot $ AC.
Suy ra AC // MN // BD.
5B. a) b) Tương tự 5A.
c) Vì OI, OJ cùng là phân giác của $ \displaystyle \widehat{{xOy}}$ nên ba điểm O, I, J thẳng hàng.
6A. a) $ \displaystyle \Delta $BEC có trung tuyến
ME = $ \displaystyle \dfrac{1}{2}$ BC => $ \displaystyle \Delta $BEC vuông tại E..Mặt khác
$ \displaystyle \Delta $BME vuông cân tại M nên $ \displaystyle \widehat{{MBE}}$ = 45°
=> $ \displaystyle \Delta $BEC vuông cân tại E.
b) Từ ý (a) suy ra BE = CE. (1)
AB $ \displaystyle \bot $AC, EK $ \displaystyle \bot $AC => AB // EK.
Mà EH $ \displaystyle \bot $ AB nên EH $ \displaystyle \bot $EK => $ \displaystyle \widehat{{HEK}}$ = 90°
=> $ \displaystyle \widehat{{HEB}}=\widehat{{KEC}}$(cùng phụ $ \displaystyle \widehat{{HEC}}$). (2)
c) Từ (1) và (2) suy ra $ \displaystyle \Delta $BHE = $ \displaystyle \Delta $CKE (Ch-gn)
=> EH – EK.
Chứng minh được $ \displaystyle \Delta $AHE = $ \displaystyle \Delta $AKE => $ \displaystyle \widehat{{HAE}}=\widehat{{KAE}}$. Vậy AE là tia phân giác của góc A.
6B. Tương tự 6A.
Chứng minh được $ \displaystyle \Delta $BID = $ \displaystyle \Delta $CHD => DI = DH.
Suy ra $ \displaystyle \Delta $ADI = $ \displaystyle \Delta $ADH =>$ \displaystyle \widehat{{DAI}}=\widehat{{DAH}}$
Vậy AD là tia phân giác của $ \displaystyle \widehat{A}$

