KIẾN THỨC CẦN NHỚ
1. Tỉ lệ bản đồ
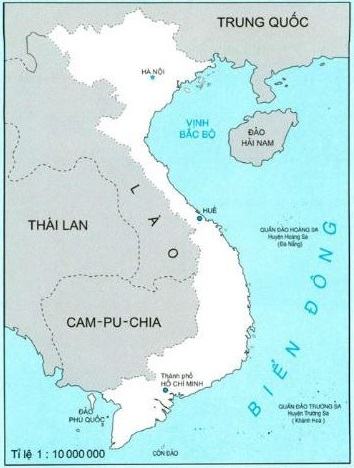
Ở góc phía dưới của bản đồ nước Việt Nam có ghi: Tỉ lệ $1\colon 10000000$. Tỉ lệ đó là tỉ lệ bản đồ.
– Tỉ lệ $1 : 10 000 000$ hay $\displaystyle\frac{1}{10000000}$ cho biết hình nước Việt Nam được vẽ thu nhỏ lại $10 000 000$ lần. Chẳng hạn: độ dài $1 cm$ trên bản đồ ứng với độ dài thật là $10 000 000 cm$ hay $100 km$.
– Tỉ lệ bản đồ có thể viết dưới dạng một phân số có tử số là $1$.
Ví dụ: $\displaystyle\frac{1}{1000} ; \quad \frac{1}{500} \quad ; \frac{1}{1000000}$
2. Ứng dụng của tỉ lệ bản đồ
a) Tính độ dài thật
Bài toán 1: Bản đồ trường Mầm non xã Thắng Lợi vẽ theo tỉ lệ $1 : 300$.
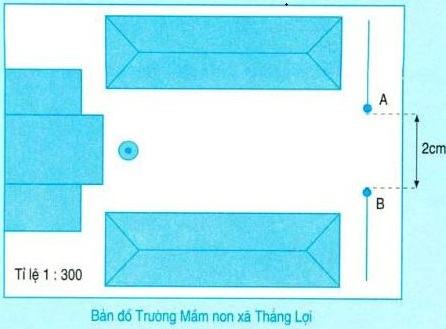
Trên bản đồ, cổng trường rộng $2 cm$ (khoảng cách từ A đến B). Hỏi chiều rộng thật của cổng trường là mấy mét ?
Bài toán:
Chiều dài thật của cổng trường là:
$2 \times 300=600(cm)$
$600 cm=6 m$
Đáp số: $6 m$
Bài toán 2: Trên bản đồ tỉ lệ $1 : 1 000 000$, quãng đường Hà Nội – Hải Phòng đó được $102 mm$. Tìm độ dài thật của quãng đường Hà Nội – Hải Phòng.
Bài giải:
Quãng đường Hà Nội – Hải Phòng dài là:
$102 \times 1000000=102000000 mm$
$10200000 mm = 102 km$
Đáp số: $102 km$
b) Tính độ dài thu nhỏ trên bản đồ
Bài toán 3: Khoảng cách giữa hai điểm A và B trên sân trường là $20 m$. Trêm bản đồ tỉ lệ $1 : 500$, khoảng cách giữa hai điểm đó là mấy xăng-ti-mét ?
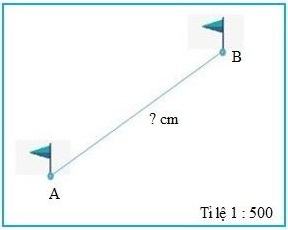
Bài giải:
$20 m=2000 cm$
Khoảng cách giữa hai điểm A và B trên bản đồ là:
$2000\colon 500=4(cm)$
Đáp số: $4 cm$
Bài toán 4: Quãng đường từ trung tâm Hà Nội đến Sơn Tây là $41 km$. Trên bản đồ tỉ lệ $1 : 1 000 000$, quãng đường đó dài bao nhiêu mi-li-mét ?
Bài giải:
$41 km=41000000 mm$
Quãng đường từ trung tâm Hà Nội đến Sơn Tây trên bản đồ dài là:
$41000000\colon 1000000=41(mm)$
Đáp số: $41 mm$

