Các công thức hệ thức lượng trong tam giác mà học sinh lớp 10 phải nhớ để áp dụng vào làm bài tập.
ĐỊNH LÝ COSIN
Trong tam giác $ABC$ với $BC = a$, $AC = b$ và $AB = c$. Ta có:
${a^2} = {b^2} + {c^2} – 2bc.\cos A.$
${b^2} = {c^2} + {a^2} – 2ca.\cos B.$
${c^2} = {a^2} + {b^2} – 2ab.\cos C.$
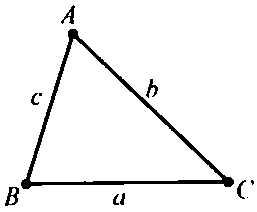
Hệ quả:
$ \displaystyle\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}}$
$ \displaystyle\cos B = \frac{{{c^2} + {a^2} – {b^2}}}{{2ca}}$
$ \displaystyle\cos C = \frac{{{a^2} + {b^2} – {c^2}}}{{2ab}}$
ĐỊNH LÝ SIN
Trong tam giác $ABC$ với $BC = a$, $AC = b$, $AB = c$ và $R$ là bán kính đường tròn ngoại tiếp.
Ta có: $ \displaystyle\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.$
ĐỘ DÀI TRUNG TUYẾN
Cho tam giác $ABC$ với ${m_a}$, ${m_b}$, ${m_c}$ lần lượt là các trung tuyến kẻ từ $A$, $B$, $C$.
Ta có:
$ \displaystyle m_{a}^{2}=\frac{{2\left( {{{b}^{2}}+{{c}^{2}}} \right)-{{a}^{2}}}}{4}$.
$ \displaystyle m_b^2 = \frac{{2\left( {{a^2} + {c^2}} \right) – {b^2}}}{4}$
$ \displaystyle m_c^2 = \frac{{2\left( {{a^2} + {b^2}} \right) – {c^2}}}{4}$
DIỆN TÍCH TAM GIÁC
Với tam giác $ABC$ ta kí hiệu ${h_a}$, ${h_b}$, ${h_c}$ là độ dài đường cao lần lượt tương ứng với các cạnh $BC$, $CA$, $AB$, $R$, $r$ lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp tam giác, $ \displaystyle P = \frac{{a + b + c}}{2}$ là nửa chu vi tam giác, $S$ là diện tích tam giác. Khi đó ta có:
$\displaystyle S=\frac{1}{2}a{{h}_{a}}=\frac{1}{2}b{{h}_{b}}=\frac{1}{2}c{{h}_{c}}=\frac{1}{2}bc\sin A=\frac{1}{2}ca\sin B=\frac{1}{2}ab\sin C=\frac{{abc}}{{4R}}=$
=$\displaystyle pr=\sqrt{{p(p-a)(p-b)(p-c)}}$(công thức Hê-rông).

