Hướng dẫn học sinh giải bài tập sách giáo khoa toán lớp 7 tập 1 trang 7, 8. Bài học Tập hợp Q các số hữu tỉ.
Bài 1. (Trang 7 SGK Toán 7 – Tập 1)
Điền ký hiệu ($\displaystyle\in ,\notin ,\subset $) thích hợp vào chỗ chấm:
$-3 \ldots \mathbb{N}$ $3 \ldots \mathbb{Z}$ $3 \ldots \mathbb{Q}$
$\displaystyle\frac{-2}{3} \ldots \mathbb{Z}$ $\displaystyle\frac{-2}{3} \ldots \mathbb{Q}$ $\displaystyle\mathbb{N} \ldots \mathbb{Z} \ldots \mathbb{Q}$
Bài giải:
Ta có:
$-3 \notin \mathbb{N}$; $-3 \in \mathbb{Z}$; $-3 \in \mathbb{Q}$;
$\displaystyle\frac{-2}{3} \notin \mathbb{Z}$; $\displaystyle\frac{-2}{3} \in \mathbb{Q}$; $\displaystyle\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q}$
Bài 2. (Trang 7 SGK Toán 7 – Tập 1)
a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ $\displaystyle\frac{3}{-4}$:
$\displaystyle\frac{-12}{15}, \frac{-15}{20}, \frac{24}{-32}, \quad \frac{-20}{28}, \quad \frac{-27}{36} ?$
b) Biểu diễn số hữu tỉ $\displaystyle\frac{3}{-4}$ trên trục số.
Bài giải
a) Ta có:
$\displaystyle\frac{-15}{20}=\frac{(-15)\colon 5}{20\colon 5}=\frac{-3}{4}=\frac{3}{-4}$
$\displaystyle\frac{-27}{36}=\frac{(-27)\colon 9}{36\colon 9}=\frac{-3}{4}=\frac{3}{-4}$
$\displaystyle\frac{24}{-32}=\frac{24\colon 8}{(-32)\colon 8}=\frac{-3}{4}$
b) Ta biểu diễn trên trục số như sau:
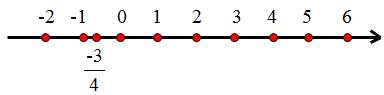
Bài 3. (Trang 8 SGK Toán 7 – Tập 1)
So sánh các số hữu tỉ:
a) $\displaystyle x=\frac{2}{-7}$ và $\displaystyle y=\frac{-3}{11}$;
b) $\displaystyle x=\frac{-213}{300}$ và $\displaystyle y=\frac{18}{-25}$;
c) $\displaystyle x=-0,75$ và $\displaystyle y=\frac{-3}{4}$.
Bài giải
a) Với $\displaystyle x=\frac{2}{-7}=\frac{-2}{7}$và $\displaystyle y=\frac{-3}{11}$;
Ta quy đồng mẫu số:
$\displaystyle x=\frac{2}{-7}=\frac{-22}{77}$
$y=\frac{-3}{11}=\frac{-21}{77}$
Ta có: $-22<-21$. Do đó $\displaystyle x<y$.
b) Với:
$\displaystyle x=\frac{-213}{300}$
$\displaystyle y=\frac{18}{-25}=\frac{-18}{25}=\frac{-216}{300}$
Ta có: $-216<-213$. Do đó $\displaystyle x>y$.
c) Với:
$\displaystyle x=-0,75$
$\displaystyle y=\frac{-3}{4}=-0,75$
Ta có: $-0,75=-0,75$. Do đó $\displaystyle x=y$.
Bài 4. (Trang 8 SGK Toán 7 – Tập 1)
So sánh số hữu tỉ $\displaystyle\frac{a}{b}(a, b \in \mathbb{Z}, b \neq 0)$ với số 0 khi $a, b$ cùng dấu và khi $a, b$ khác dấu.
Bài giải
Theo đề bài ta có $\displaystyle\frac{a}{b}(a, b \in \mathbb{Z}, b \neq 0)$
a) Khi a và b cùng dấu mà $b>0$ thì $a>0$. Do đó số hữu tỉ $\displaystyle\frac{a}{b}>0$.
b) Khi a và b khác dấu mà $b>0$, do đó $a<0$. Do đó số hữu tỉ $\displaystyle\frac{a}{b}<0$.
Bài 5. (Trang 8 SGK Toán 7 – Tập 1)
Giả sử $\displaystyle x=\frac{a}{m}, y=\frac{b}{m}(a, b, m \in Z, m>0)$ và $\displaystyle x<y$.
Hãy chứng tỏ rằng nếu chọn $\displaystyle z=\frac{a+b}{2 m}$ thì ta có $\displaystyle x<z<y$.
Hướng dẫn: Sử dụng tính chất:
Nếu $a, b, c \in Z$ và $a<b$ thì $a+c<b+c \cdot $
Bài giải
Ta có: $\displaystyle x=\frac{a}{m}, y=\frac{b}{m}(a, b, m \in Z, m>0)$
Và $\displaystyle x<y$. Do đó $a<b$, suy ra: $a m<b m$
Ta chứng minh $\displaystyle x<z$ hay $\displaystyle\frac{a}{m}<\frac{a+b}{2 m}$
Ta có: $a m<b m \Rightarrow a m+a m<b m+a m$ (cộng cả hai vế với am)
$\displaystyle\Rightarrow 2 a m<(a+b) m \Rightarrow a<\frac{(a+b) m}{2 m}$
$\displaystyle\Rightarrow \frac{a}{m}<\frac{a+b}{2 m}$ (chia cả 2 vế cho m > 0 )
Vậy $\displaystyle x<z$ (1)
Ta chứng minh $z<y$ hay $\displaystyle\frac{a+b}{2 m}<\frac{b}{m}$
Ta có: $a m<b m \Rightarrow a m+b m<b m+b m$ (cộng 2 vế với bm)
$\displaystyle\Rightarrow(a+b) m<2 b m$
$\displaystyle\Rightarrow a+b<2 b$ ( chia cả 2 vế cho m)
$\displaystyle\Rightarrow \frac{a+b}{2 m}<\frac{2 b}{2 m}=\frac{b}{m}$ ( chia cả 2 vế cho 2m )
Hay $z<y$ (2)
Từ (1) và (2) suy ra: $\displaystyle x<z<y$.

