KIẾN THỨC CẦN NHỚ
Thể tích hình hộp chữ nhật
Quy tắc: Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng đơn vị đo).
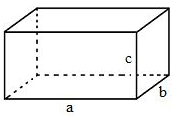
Gọi $V$ là thể tích của hình hộp chữ nhật, ta có: $V=a \times b \times c$ ($a, b, c$ là ba kích thước của hình hộp chữ nhật).
Lưu ý: Chiều dài nhân với chiều rộng chính là diện tích đáy. Vậy có thể tính thể tích hình hộp chữ nhật bằng cách lấy diện tích đáy nhân với chiều cao.
CÁC DẠNG TOÁN
Dạng 1: Tính thể tích hình hộp chữ nhật khi biết ba kích thước
Phương pháp: Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng đơn vị đo).
Dạng 2: Tính chiều cao của hình hộp chữ nhật
Phương pháp: Chiều cao của hình hộp chữ nhật chia cho diện tích:
$c=V\colon (a \times b)$
Dạng 3: Tính diện tích đáy khi biết thể tích
Phương pháp: Diện tích đáy của hình hộp chữ nhật bằng thể tích chia cho chiều cao:
$a \times b=V\colon c$
Dạng 4: Toán có lời văn (thường tính thể tích nước, chiều cao mực nước,…)
Phướng pháp: Đọc kĩ đề bài, xác định dạng toán và yêu cầu của đề bài rồi giải bài toán đó.
BÀI TẬP VÍ DỤ
Ví dụ 1: Tính thể tích hình hộp chữ nhật có chiều dài $14 \mathrm{~cm}$, chiều rộng $7 \mathrm{~cm}$ và chiều cao $8 \mathrm{~cm}$.
Bài giải
Thể tích của hình hộp chữ nhật đó là:
$14 \times 7 \times 8=784\left(\mathrm{~cm}^{3}\right)$
Đáp số: $784 \mathrm{~cm}^{3}$
Ví dụ 2: Một hình hộp chữ nhật có thể tích bằng $468 \mathrm{~cm}^{3}$, chiều dài bằng $12 \mathrm{~cm}$, chiều rộng bằng $6 \mathrm{~cm}$. Hỏi hình hộp chữ nhật đó cao bao nhiên xăng-ti-mét ?
Bài giải
Chiều cao của hình hộp chữ nhật đó là:
$468\colon (12 \times 6)=6,5(\mathrm{~cm})$
Đáp số: $6,5 \mathrm{~cm}$

