Phiếu bài tập cuối tuần môn Toán lớp 8 – Tuần 2: Những hằng đẳng thức đáng nhớ. Hình thang cân.
Bài 1: Tính:
$ a)~\left( 3b+\dfrac {5a}{6} \right)^2$ $ b)( 5x-y )^2$
$ c)( 2a+b-5 )( 2a-b+5 )$ $ d)\left( x^2+\dfrac {2}{5}y \right)\left( x^2-\dfrac {2}{5}y \right)$
Bài 2: Viết các đa thức sau dưới dạng bình phương của một tổng hoặc một hiệu:
$ a)~a^2-6a+9$ $ b)\dfrac {1}{4}x^2+2xy^2+4y^4$
Bài 3: Rút gọn biểu thức:
a) $( a+1 )^2-( a-1 )^2-3( a+1 )( a-1 );$
b) $( m^3-m+1 )^2+( m^2-3 )^2-2( m^2-3 )( m^3-m+1 ) $
Bài 4: Tìm x, biết:
a) $( 3x-5 )( 5-3x )+9( x+1 )^2=30;$
b) $( x+4 )^2-( x+1 )( x-1 )=16 $
Bài 5: So sánh hai số A và B:
a) $A=( 3+1 )( 3^2+1 )( 3^4+1 )( 3^8+1 )( 3^{16}+1 )$ và $B=3^{32}-1$;
b) $A=2011\cdot 2013$ và $B=2012^2 $
Bài 6: Cho hình thang cân ABCD ( AB//CD) có $\hat{D}=70^o$
a) Tính số đo các góc $\hat{B};~\!\!~\!\!\hat{C};~\hat{A}$
b) Kẻ đường cao AH và BK của hình thang. Chứng minh DH = CK
Bài 7: Cho tam giác ABC cân tại, kẻ phân giác BE, CF của các góc B và C.
a) Chứng minh tam giác AEF cân
b) Chứng minh ΔBFC = ΔCEB
c) Chứng minh BFEC là hình thang cân
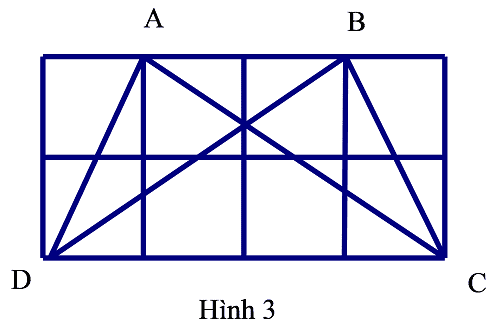
Bài 8: Cho hình 3. Tính độ dài các cạnh và đường chéo của hình thang cân ABCD (độ dài cạnh hình vuông là 1cm).
Bài 9: Cho hình thang ABCD ( AB//CD, AB<CD). Hai tia phân giác của hai góc C và D cắt nhau tại K thuộc đáy AB. Chứng minh:
a) Tam giác ADK cân tại A; tam giác BKC cân tại B
b) AD + BC = AB
Bài 10: Cho hình thang ABCD ( AB//CD) có CD = AD + BC. Gọi K là giao điểm của tia phân giác góc A với đáy CD. Chứng minh:
a) AD = DK
b) Tam giác BKC cân tại C
c) BK là tia phân giác góc B
* Download file word: PHIẾU BÀI TẬP TOÁN LỚP 8 – TUẦN 2.docx bằng cách click vào nút Tải về dưới đây:

