Phiếu bài tập cuối tuần môn Toán lớp 8 – Tuần 5: Phân tích đa thức thành nhân tử. Đối xứng trục.
Bài 1: Phân tích các đa thức sau thành nhân tử:
$ a)~48x^3y^3-32x^2y^2;$ $ b)~ax-bx+ab-x^2;$
$ c)~12a^2b-18ab^2-30b^2;$ $ d)~27a^2( b-1 )-9a^3( 1-b ) $
Bài 2: Tìm x, biết:
$ a)~5( x+3 )-2x( 3+x )=0;$ $ b)~6x( x^2-2 )-( 2-x^2 )=0;$
$ c)~4x( x-2013 )-x+2013=0;$ $ d)~( x+1 )^2=x+1 $
Bài 3: Chứng minh rằng với mọi số nguyên a thì $ a^2( a+1 )+2a( a+1 )$ chia hết cho 6.
Bài 4: Tính giá trị của các biểu thức sau:
$ a)~A=2m( n-p )+( p-n )( m+q )$ với m = 18,3 ; n = 24,6 ; p = 10,6 ; q = -31,7.
$ b)~B=( a-b )( b+c )+b( b-a )$ với a = 0,86 ; b = 0,26 ; c = 1,5.
$ c)~C=a( b-c )+2( c-b )$ với a = 2 ; b = 1,007 ; c = -0,006.
Bài 5: Tính:
$ a)~A=\dfrac {298^3+48^3}{346}-298\cdot 48$
$ b)~B=\dfrac {526^3-474^3}{52}+526\cdot 474$
Bài 6: Cho $\widehat{xOy}<90^o,$ điểm A nằm trong góc đó. Gọi B là điểm đối xứng với A qua điểm Ox, C là điểm đối xứng với A qua Oy.
a) Chứng minh OBC là tam giác cân
b) Cho $\widehat{xOy}=70^o $ Tính $\widehat{BOC}$
Bài 7: Cho hai điểm A và B nằm cùng phía đối với đường thằng d. Gọi M và N là hai điểm đối xứng với A và B qua d.
a) TỨ giác ABNM là gì?
b) BM cắt d tại C, lấy điểm D bất kì trên d ($D\ne C) $. Chứng minh $BD+MN>BC+CA$
Bài 8: Cho hình thang ABCD (AB//CD) và AB < CD, DA cắt CB tại I
a) Chứng minh IAB là tam giác cân
b) Chứng minh $\Delta IB\mathrm{\,d}=\triangle IAC$
c) AC cắt BD tại K. Chứng minh $\Delta K\text{AD}=\triangle KBC$
d) Chứng minh IK là trục đối xứng của hình thang ABCD.
Bài 9: Vẽ hình đối xứng với hình đã cho qua đường thẳng d:
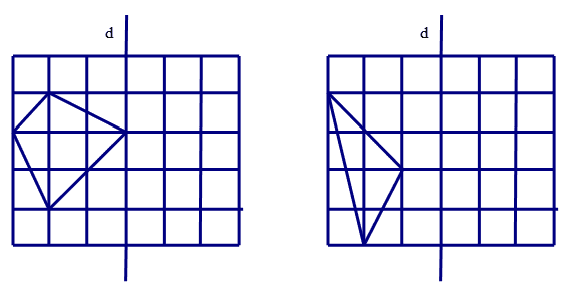
Bài 10: Cho hai điểm A và B nằm cùng phía đối với đường thẳng a. Hãy tìm trên a một điểm M sao cho $AM+MB$ là bé nhất.
* Download file word: PHIẾU BÀI TẬP TOÁN LỚP 8 – TUẦN 5.docx bằng cách click vào nút Tải về dưới đây:

