KIẾN THỨC CẦN NHỚ
1. Ôn lại phân số thập phân
Các phân số có mẫu số là $10 ; 100 ; 1000 ; \ldots$ được gọi là các phân số thập phân
Ví dụ: $\displaystyle\frac{1}{10} ; \frac{6}{10}$ là các phân số thập phân.
2. Khái niệm số thập phân, cấu tạo số thập phân
a. Khái niệm số thập phân
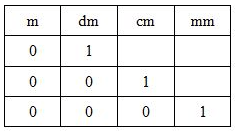
+) $1 d m$ hay $\displaystyle\frac{1}{10} m$ còn được viết thành $0,1 \mathrm{~m}$
+) $1 \mathrm{~cm}$ hay $\displaystyle\frac{1}{100} m$ còn được viết thành $0,01 \mathrm{~m}$
+) $1 \mathrm{~mm}$ hay $\displaystyle\frac{1}{1000} m$ còn được viết thành $0,001 \mathrm{~m}$.
Các phân số thập phân $\displaystyle\frac{1}{10} ; \frac{1}{100} ; \frac{1}{1000}$ được viết thành $0,1 ; 0,01 ; 0,001$.
0,1 đọc là: không phẩy một; $\displaystyle 0,1=\frac{1}{10}$
0,01 đọc là: không phẩy không một; $\displaystyle 0,1=\frac{1}{100}$
0,001 đọc là: không phẩy không không một; $\displaystyle 0,001=\frac{1}{1000}$
Tương tự, các phân số thập phân $\displaystyle\frac{3}{10} ; \frac{5}{100} ; \frac{8}{1000}$ được viết thành 0,$3 ; 0,5 ; 0,008$
$\displaystyle\frac{3}{10}=0,3 ; \frac{5}{100}=0,05 ; \frac{8}{1000}=0,008$
Các số $0,3; 0,05; 0,008$ cũng là số thập phân.
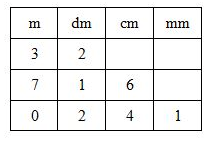
+) $3 \mathrm{~m} 2 \mathrm{dm}$ hay $\displaystyle 3 \frac{2}{10} \mathrm{~m}$ được viết thành $3,2 \mathrm{~m}$. $3,2 \mathrm{~m}$ đọc là: ba phấy hai mét.
+) $7 \mathrm{~m} 16 \mathrm{~cm}$ hay $\displaystyle 7 \frac{16}{100} \mathrm{~m}$ được viết thành $7,16 \mathrm{~m}$. $7,16 \mathrm{~m}$ đọc là: bảy phầy mười sáu mét.
+) $0 \mathrm{~m} 241 \mathrm{~mm}$ hay $0 \mathrm{~m}$ và $\displaystyle\frac{241}{1000} \mathrm{~m}$ được viết thành $0,241 \mathrm{~m}$. $0,241 \mathrm{~m}$ đọc là: không phấy hai trăm bốn mươi mốt mét.
Các số $3,2 ; 7,16 ; 0,241$ cũng là số thập phân
b. Cấu tạo số thập phân
Mỗi số thập phân gồm hai phần: Phần nguyên và phần thập phân, chúng được phân cách bởi dấu phẩy.
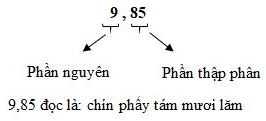
Những chứ số ở bên trái dấu phẩy thuộc về phần nguyên, những chữ số ở bên trái dấu phẩy thuộc về phần thập phân.
CÁC DẠNG TOÁN
Dạng 1: Chuyển các phân số thành số thập phân
Phương pháp: Nếu phân số đã cho chưa là số thập phân thì ta chuyển các phân số thành phân số thập phân rồi chuyển thành số thập phân.
Mẹo: Khi chuyển phân số thập phân thành số thập phân, ta đếm xem mẫu số có bao nhiêu sữ số 0 thì phần thập phân của số thập phân cũng có bấy nhiêu chữ số.
Dạng 2: Viết các số đo độ dài, khối lượng… dưới dạng số thập phân
Phương pháp:
– Tìm mối liên hệ giữa hai đơn vị đo đã cho.
– Chuyển số đo độ dài đã cho thành phân số thập phân có đơn vị đo lớn hơn.
– Chuyển từ số đo độ dài dưới dạng phân số thập phân thành số đo độ dài tương ứng dưới dạng số thập phân có đơn vị lớn hơn.
Dạng 3: Viết hỗn số thành số thập phân
Phương pháp: Đổi hỗn số về dạng phân số thập phân, sau đó chuyển thành số thập phân.
Dạng 4: Chuyển các số thập phân thành phân số thập phân
Phương pháp:
– Phân số thập phân có mẫu số là
– Nếu phần nguyên của số thập phân bằng 0 thì phân số thập phân có tử số nhỏ hơn mẫu số, nếu phần nguyên lớn hơn 0 thì tử số lớn hơn mẫu số.
– Số thập phân đã cho ở phần thập phân (bên phải dấu phẩy) có bao nhiêu chữ số thì khi chuyển sang phân số thập phân ở mẫu số cũng sẽ có bấy nhiêu chữ số 0
BÀI TẬP VÍ DỤ
Ví dụ 1: Chuyển các phân số sau thành số thập phân:
a) $\displaystyle\frac{7}{10}$
b) $\displaystyle\frac{3}{100}$.
c) $\displaystyle\frac{2}{5}$.
Bài giải:
a) $\displaystyle\frac{7}{10}=0,7$
b) $\displaystyle\frac{3}{100}=0,03$
c) $\displaystyle\frac{2}{5}=\frac{2 \times 2}{5 \times 2}=\frac{4}{10}=0,4$
Ví dụ 2: Điền phân số thập phân và số thập phân thích hợp vào chỗ trống
a) $4 \mathrm{~cm}=\frac{4}{10} d m=\ldots d m$
b) $3 \mathrm{~cm}=\ldots m=\ldots m$
Bài giải:
a) $\displaystyle 4 c m=\frac{4}{10} d m=0,2 d m$
b) $\displaystyle 3 c m=\frac{3}{100} m=0,03 m$
Ví dụ 3: Viết hỗn số sau thành số thập phân:
a) $\displaystyle 3 \frac{7}{10}$
b) $\displaystyle 5 \frac{7}{20}$
Bài giải:
a) $\displaystyle 3 \frac{7}{10}=\frac{37}{10}=3,7$
b) $\displaystyle 5 \frac{7}{20}=5 \frac{35}{100}=\frac{535}{100}=5,35$
Ví dụ 4: Chuyển các số thập phân sau thành phân số thập phân: 0,$5 ; 0,03 ; 21,564$.
Bài giải:
$\displaystyle 0,5=\frac{5}{10}$
$\displaystyle 0,03=\frac{3}{100}$
$\displaystyle 21,564=\frac{21564}{1000}$

