KIẾN THỨC CẦN NHỚ
Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
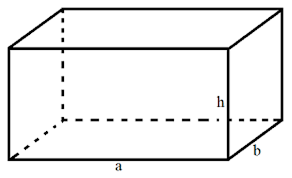
a) Định nghĩa
– Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích bốn mặt bên của hình hộp chữ nhật.
– Diện tích toàn phần của hình hộp chữ nhật là tổng của diện tích xung quanh và diện tích đáy.
b) Quy tắc
Giả sử hình hộp chữ nhật có chiều dài là $a$, chiều rộng là $b$ và chiều cao là $h$.
– Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng đơn vị đo).
$S_{x q}=(a+b) \times 2 \times h$
– Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
$ \displaystyle S_{{tp}}=S_{{xq}}+S_{{day}}\times 2=(a+b)\times 2\times h+2\times a\times b$
Lưu ý:
– Chu vi mặt đáy bằng tổng của chiều dài và chiều rộng nhân với $2$.
– Diện tích mặt đáy bằng tích của chiều dài và chiều rộng.
CÁC DẠNG TOÁN
Dạng 1: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
Phương pháp: Áp dụng quy tắc tính diện tích xung quanh hoặc diện tích toàn phần.
Dạng 2: Biết diện tích xung quanh hoặc diện tích toàn phần, tìm chu vi đáy hoặc chiều cao của hình hộp chữ nhật
Phương pháp:
*) Từ công thức $S_{x q}=(a+b) \times 2 \times h$
– Tìm chiều cao $h$ theo công thức: $h=S_{x q}\colon [(a+b) \times 2]=S_{x q}\colon (a+b)\colon 2$
– Tìm tổng chu vi đáy theo công thức: $(a+b) \times 2=S_{x q}\colon h$
*) Nếu biết diện tích toàn phần ta cũng thay vào công thức để tì các đại lượng chưa biết.
Dạng 3: Toán có lời văn (thường là tìm diện tích hộp, căn phòng, sơn tường, …)
Phương pháp: Cần xác định xem diện tích cần tìm là diện tích xung quanh hay diện tích toàn phần rồi áp dụng quy tắc tính diện tích xung quanh hoặc diện tích toàn phần.
BÀI TẬP VÍ DỤ
Ví dụ 1: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài $6cm$, chiều rộng bằng $5cm$ và chiều cao $4cm$.
Bài giải
Chu vi đáy của hình hộp chữ nhật là:
$(6+5) \times 2=22(\mathrm{~cm})$
Diện tích xung quanh của hình hộp chữ nhật đó là:
$22 \times 4=88\left(\mathrm{~cm}^{2}\right)$
Diện tích một đáy là:
$6 \times 5=30\left(\mathrm{~cm}^{2}\right)$
Diện tích toàn phần của hình hộp chữ nhật đó là:
$88+30 \times 2=148\left(\mathrm{~cm}^{2}\right)$
Đáp số: Diện tích xung quanh: $88 cm^{2}$
Diện tích toàn phần: $148 cm^{2}$
Ví dụ 2: Cho hình hộp chữ nhật có diện tích xung quanh $196 m^{2}$ và có nửa chu vi mặt đáy bằng $14m$. Tính chiều cao của hình hộp chữ nhật đó.
Bài giải
Chu vi mặt đáy của hình hộp chữ nhật đó là:
$14 \times 2=28(m)$
Chiều cao của hình hộp chữ nhật đó là:
$196\colon 28=7(m)$
Đáp số: $7m$
Ví dụ 3: Một căn phòng dạng hình hộp chữ nhật có chiều dài $5m$, chiều rộng $4,2m$, chiều cao $4m$. Người ta muốn quét vôi tường xung quanh và trần căn phòng đó. Hỏi diện tích cần quét là bao nhiêu mét vuông, biết tổng diện tích các cửa bằng $12 m^{2}$. (Chỉ quét vôi bên trong phòng).
Bài giải
Diện tích xung quanh căn phòng đó là:
$(5+4,2) \times 2 \times 4=73,6\left(m^{2}\right)$
Diện tích trần của căn phòng đó là:
$6 \times 4,2=25,2\left(m^{2}\right)$
Diện tích cần quét vôi là:
$73,6+25,2-12=86,8\left(m^{2}\right)$
Đáp số: $86,8 m^{2}$

