LÝ THUYẾT
Phương pháp 1
Cơ sở của phương pháp tìm giao tuyến của hai mặt phẳng $(\alpha)$ và $(\beta)$ cần thực hiện:
– Bước 1: Tìm hai điểm chung $\mathrm{A}$ và $\mathrm{B}$ của $\alpha$ và $(\beta)$.
– Bước 2: Đường thẳng $\mathrm{AB}$ là giao tuyến cần tìm $(A B=(\alpha) \cap(\beta))$.
Chú ý Để tìm chung của $(\alpha)$ và $(\beta)$ thường tìm 2 đường thẳng đồng phẳng lần lượt nằm trong hai mp giao điểm nếu có của hai đường thẳng này là điểm chung của hai mặt phẳng.
Phương pháp 2
Tương tự phương pháp 1 khi chỉ tìm ngay được 1 điểm chung $S$.
Lúc này ta có hai trường hợp:
– TH1: Hai mặt phẳng $(\alpha)$ và $(\beta)$ theo thứ tự chứa hai đường thẳng $d_{1}$ và $d_{2}$ mà $d_{1} \cap d_{2}=I$.
$\Rightarrow S I$ là giao tuyến cần tìm (tức là $(\alpha) \cap(\beta))=S I$ )
– $\mathrm{TH} 2$ : Hai mặt phẳng $(\alpha)$ và $(\beta)$ lần lượt chứa hai đường thẳng $d_{1}$ và $d_{2}$ mà $d_{1} / / d_{2}$.
Dựng $x S y$ song song với $d_{1}$ hoặc $d_{2}$.
$\Rightarrow x S y$ là giao tuyến cần tìm. (tức là $(\alpha) \cap(\beta))=x S y$ ).
BÀI TẬP CÓ LỜI GIẢI
Xem các bài tập dưới đây để biết cách tìm giao tuyến của 2 mặt phẳng trong không gian.
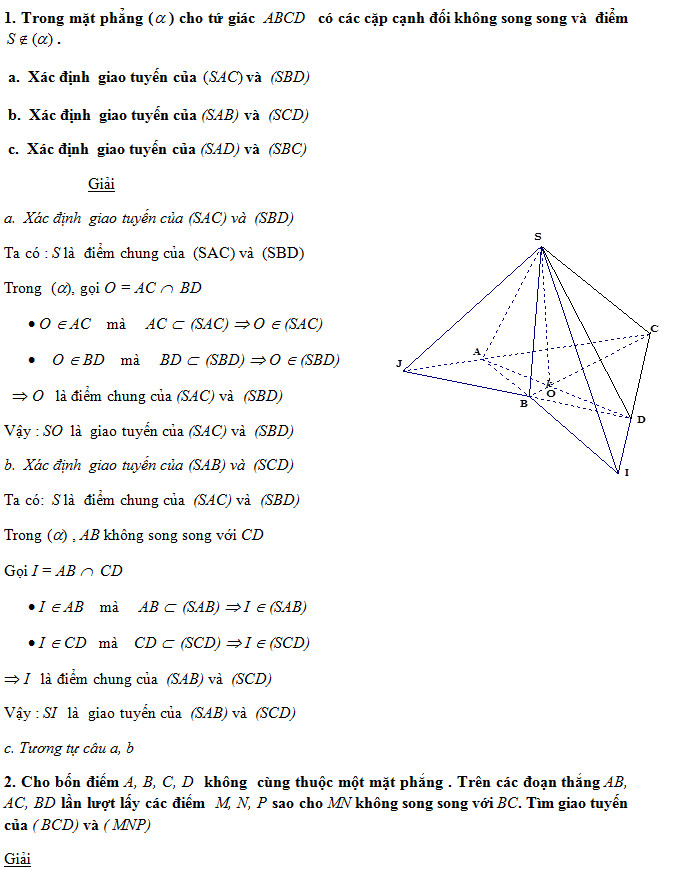
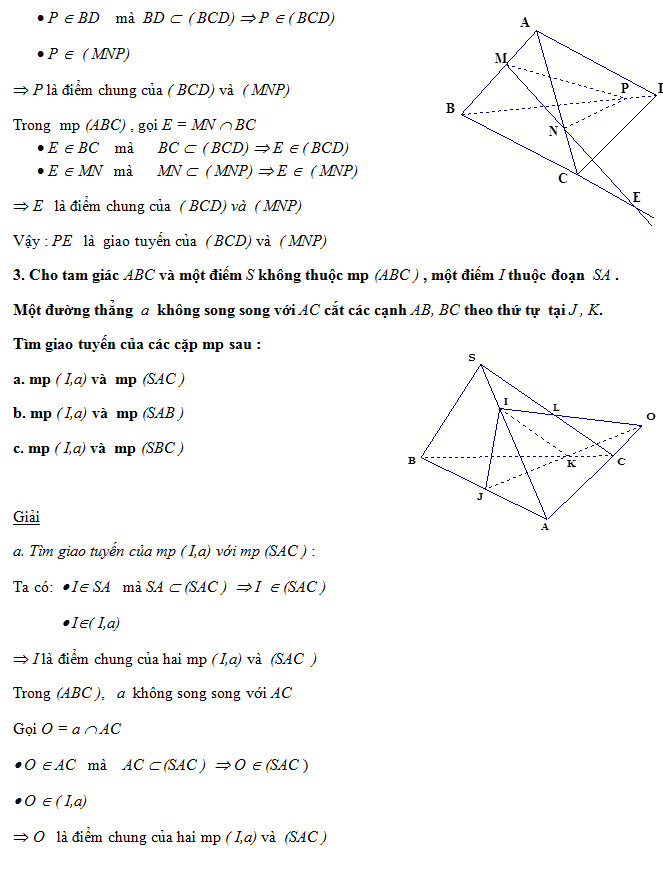

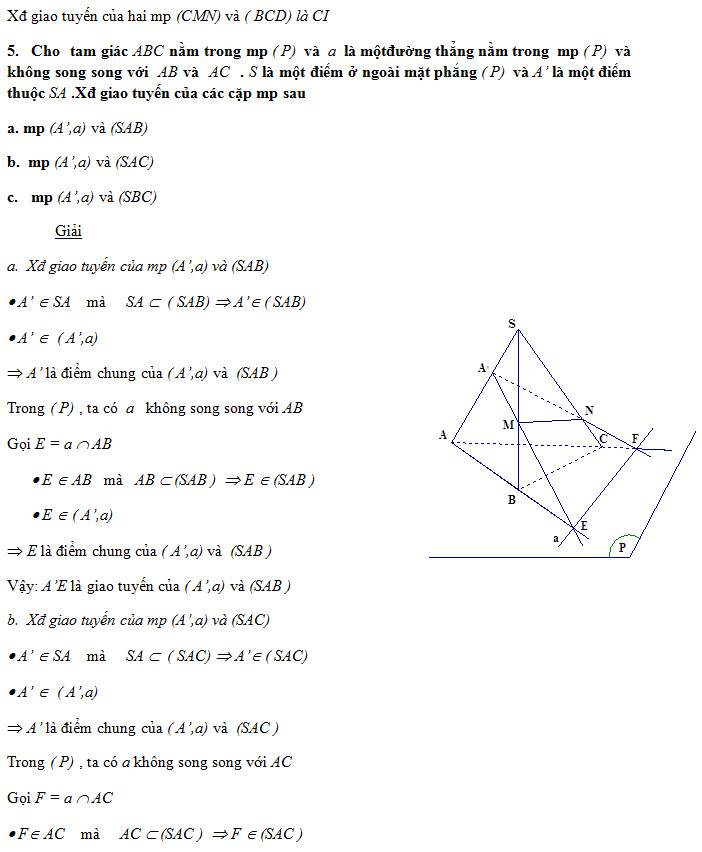
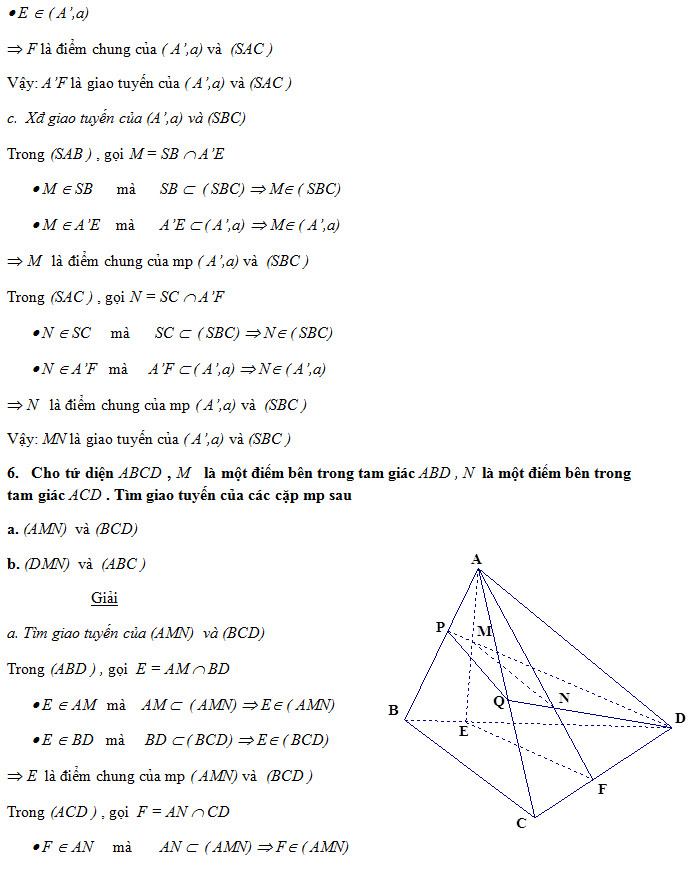

BÀI TẬP ÁP DỤNG



