A. LÝ THUYẾT
1. Định nghĩa tia phân giác của góc
Tia phân giác của một góc là tia nằm giữa hai cạnh của một góc và tạo với hai cạnh ấy hai góc bằng nhau.
2. Cách chứng minh tia Oy là tia phân giác của góc xOz
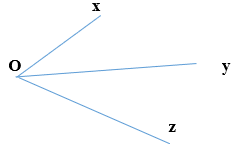
– Cách 1: Ta chứng minh $ \displaystyle \widehat{{xOy}}=\widehat{{yOz}}=\dfrac{1}{2}\widehat{{xOz}}$
– Cách 2: Ta đi chứng minh tia $Oy$ nằm giữa 2 tia $Ox$ và $Oz$ và chứng minh thêm $ \displaystyle \widehat{{xOy}}=\widehat{{yOz}}$.
B. BÀI TẬP
Bài 1: Vẽ $\widehat{A O B}=80^{\circ}$ và $OM$ là tia phân giác của $\widehat{A O B}$. Tính số đo của $\widehat{A O M}$
Bài 2: Vẽ $\widehat{A O B}=60^{\circ}$. Vẽ $OC$ sao cho $\mathrm{OB}$ là tia phân giác của $\widehat{A O C}$. Tính số đo của $\widehat{A O C}$
Bài 3: Vẽ $\widehat{A O B}=60^{\circ}$. Vẽ $OC$ sao cho $OA$ là tia phân giác của $\widehat{B O C}$. Tính số đo cùa $\widehat{A O C}$ và $\widehat{B O C}$
Bài 4: Vẽ $\widehat{A O B}, \widehat{A O C}$ kề với nhau. Biết $\widehat{A O B}=\widehat{A O C}=70^{\circ}$
1) Chứng minh tia $OA$ là tia phân giác của $\widehat{B O C}$.
2) Tính số đo của $\widehat{B O C}$
Bài 5: Vẽ $\widehat{x O y}=80^{\circ}$ và $\widehat{x O z}=85^{\circ}$ sao cho $\widehat{O D} y$ và $\widehat{x O z}$ kề nhau
1) Chứng minh tia $Ox$ là tia phân giác của $\widehat{y O z}$
2) Tính số đo của $\widehat{y O z}$
Bài 6: Trên một mặt phẳng vẽ ba tia $\mathrm{Ox}, \mathrm{Oy}, \mathrm{Oz}$ sao cho $\widehat{x O y} =70^{\circ}$ và tia $\mathrm{Oy}$ là tia phân giác của $\widehat{O} z$. Tính số đo của $\widehat{xOz}$ và $ \widehat{y O z}$
Bài 7: Trên một mặt phẳng vẽ ba tia $\mathrm{Ox}, \mathrm{Oy}, \mathrm{Oz}$ sao cho $\widehat{x O y}$ kề với $\widehat{y O} z$ và $\widehat{x O y}=\widehat{y O z}$
1) Tia $Oy$ là gì của $\widehat{x O z} ?$
2) Già sử $x \widehat{O z}=150^{\circ}$. Tính số đo $\widehat{x O y}$ và $\widehat{y O z}$
Bài 8: Vẽ $x \widehat{O} y=90^{\circ}$ có $\mathrm{OM}$ là tia phân giác của $\widehat{x O y}$. Tính số đo $\widehat{x O M}$
Bài 9: Vẽ $\widehat{A O B}=130^{\circ}$ và $\widehat{A O C}=65^{\circ}$ sao cho $\widehat{A O B}$ và $\widehat{A O C}$ không kề nhau
1) Trong ba tia $\mathrm{OA}, \mathrm{OB}, \mathrm{OC}$ tia nào nằm giữa hai tia còn lại?
2) Chứng minh tia $\mathrm{OC}$ là tia phân giác của $\widehat{A O B}$.
Bài 8: Vẽ $\widehat{x O y}=90^{\circ}$ có OM là tia phân giác của $\widehat{x O y}$. Tính số đo $\widehat{x O M}$
Bài 9: Vẽ $\widehat{A O B}=130^{\circ}$ và $\widehat{A O C}=65^{\circ}$ sao cho $\widehat{A O B}$ và $\widehat{A O C}$ không kề nhau
1) Trong ba tia $\mathrm{OA}, \mathrm{OB}, \mathrm{OC}$ tia nào nằm giữa hai tia còn lại?
2) Chứng minh tia $\mathrm{OC}$ là tia phân giác của $\widehat{A O B}$.
Bài 10: Trên một mặt phẳng vẽ ba tia $\mathrm{OA}, \mathrm{OB}, \mathrm{OC}$ sao cho $\widehat{A O C}=160^{\circ}, \widehat{B O C}=80^{\circ}$ và $\widehat{A O C}$ không kề với $\widehat{B O C}$
1) Trong ba tia $\mathrm{OA}, \mathrm{OB}, \mathrm{OC}$ tia nào nằm giữa hai tia còn lại?
2) Chứng minh tia $\mathrm{OB}$ là tia phân giác của $\widehat{A O C}$.

