Phiếu bài tập cuối tuần môn Toán lớp 8 – Tuần 16: Phép trừ các phân thức đại số- diện tích tam giác.
Bài 1: Thực hiện phép tính:
$ a)\dfrac {5-x}{x-y}+\dfrac {6-x}{x^2-y^2}-\dfrac {4-x}{x+y}$
$ b)\dfrac {1}{\left( a-b \right)\left( b-c \right)}-\dfrac {1}{\left( a-c \right)\left( b-c \right)}-\dfrac {1}{\left( a-b \right)( a-c )}$
$ c)\dfrac {5}{2y^2+6y}-\dfrac {4y-3y^3}{y^3-9y}-3$
$ d)\dfrac {y^3}{y+1}+\dfrac {y^2}{y-1}+\dfrac {1}{y+1}-\dfrac {1}{y-1}$
Bài 2: Thực hiện phép tính:
$ a)\dfrac {5}{x+1}-\dfrac {10}{x-x^2-1}-\dfrac {15}{x^3+1}$
$ b)\dfrac {1}{n( n+1 )}+\dfrac {1}{n+1}-\dfrac {1}{n}$
$ c)\dfrac {3y^2}{x^4-xy^3}+\dfrac {y}{x^3+x^2y+xy^2}-\dfrac {1}{x^2-xy}$
$ d)\dfrac {a}{x\left( x+a \right)}+\dfrac {a}{\left( x+a \right)\left( x+2a \right)}+\dfrac {a}{\left( x+2a \right)( x+3a )}+\dfrac {1}{x+3a}$
Bài 3: Tính $A=\dfrac {1}{x\left( x+1 \right)}+\dfrac {1}{\left( x+1 \right)\left( x+2 \right)}+\dfrac {1}{\left( x+2 \right)( x+3 )}+\dfrac {1}{x+3}$
Chứng minh đẳng thức $\dfrac {1}{x( x+1 )}=\dfrac {1}{x}-\dfrac {1}{x+1}$
Bài 4: Tìm m, n, p sao cho $\dfrac {1}{\left( y-1 \right)^2\left( y-2 \right)}=\dfrac {m}{y-1}+\dfrac {n}{\left( y-1 \right)^2}+\dfrac {p}{y-2}$
Bài 5: Gọi a, b, c là độ dài 3 cạnh của tam giác ABC, thỏa mãn
$\dfrac {ab}{b+c}+\dfrac {bc}{a+c}+\dfrac {ac}{a+b}=\dfrac {ac}{b+c}+\dfrac {ab}{a+c}+\dfrac {bc}{a+b}$
Chứng minh tam giác ABC cân.
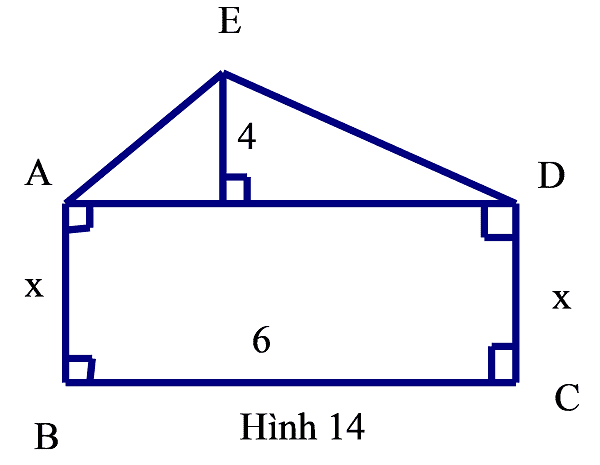
Bài 6: Cho hình vẽ 14. Tính x để $S_{ABCD}=3S_{ADE}$
Bài 7: Cho tam giác ABC, M trên cạnh BC. Chứng minh rằng $\dfrac {S_{ABM}}{S_{ACM}}=\dfrac {BM}{CM}$.
Bài 8: Cho tam giác ABC vuông cân. Một hình vuông ADEF có diện tích $361cm^2$ nội tiếp tam giác đó. Tính $S_{ABC}$
Bài 9: Hình thang ABCD (AB//CD) có $AB=6cm,~CD=9cm,$ đường cao bằng 4. Tính diện tích tam giác ADC, ABC.
Bài 10: Cho tam giác ABC có $BC=a,~AC=b,~AB=c$. Gọi I là giao điểm của các đường phân giác, d là khoảng cách từ I đến BC. Chứng minh $S_{ABC}=\dfrac {a+b+c}{2}\cdot d$.
* Download file word: PHIẾU BÀI TẬP TOÁN LỚP 8 – TUẦN 16.docx bằng cách click vào nút Tải về dưới đây:

