Đề thi chọn học sinh giỏi môn Toán lớp 9 thành phố Vinh, tỉnh Nghệ An chọn đội tuyển dự thi HSG tỉnh, năm học 2022-2023. Thời gian làm bài 150 phút.
Hình thức thi tự luận gồm 5 câu.
Hướng dẫn giải đáp án Đề thi HSG Toán 9 thành phố Vinh, Nghệ An dự thi HSG tỉnh 2022-2023
Câu 1c:
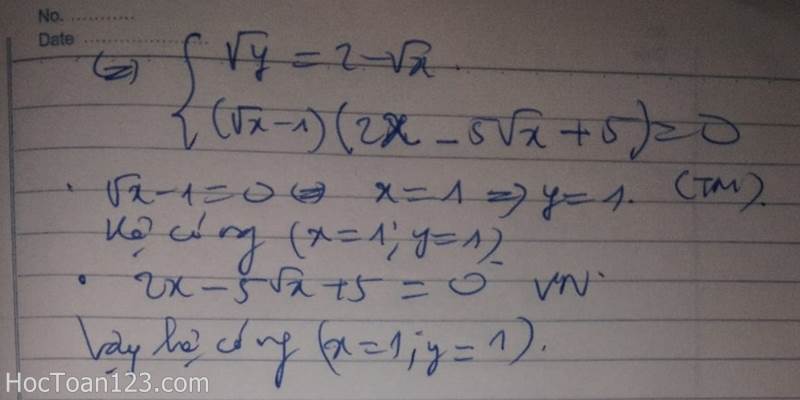
Câu 2a
Từ \(2(x+1)^2=21-3y^2\le21\), suy ra
\[(x+1)^2\le\frac{21}{2}.\]
Vì \((x+1)^2\) là số chính phương nguyên, nên \((x+1)^2\in\{0,1,4,9\}\). Xét lần lượt các trường hợp này rồi thay trở lại phương trình để tìm \(x,y\). Một cách khác là xem phương trình như phương trình bậc hai theo \(x\), sau đó dùng điều kiện biệt thức theo \(y\) để giới hạn các khả năng.
Câu 2b:
Vì p, q là các số nguyên tố lẻ. Nếu p và q đều khác 3 thì \(p,q\equiv\pm1\pmod3\), nên \(p(p+3)\equiv p^2\equiv1\pmod3\) và \(q(q+3)\equiv q^2\equiv1\pmod3\). Khi đó vế trái chia 3 dư 2, trong khi \(n(n+3)\equiv n^2\pmod3\) chỉ có thể chia 3 dư 0 hoặc 1, mâu thuẫn. Do đó một trong hai số p, q phải bằng 3.
Giả sử p=3. Ta có 18+q(q+3)=n(n+3), hay \((n-q)(n+q+3)=18\). Vì n-q>0, xét các cặp ước dương của 18 với n-q<n+q+3: (1,18), (2,9), (3,6). Tương ứng thu được (n,q)=(8,7), (4,2), (3,0). Chỉ q=7 là số nguyên tố lẻ. Vậy (p,q,n)=(3,7,8). Đổi vai trò p và q, được thêm (p,q,n)=(7,3,8).
Vậy các bộ số thỏa mãn là (3,7,8) và (7,3,8).
Câu 2c:
Câu 3a:
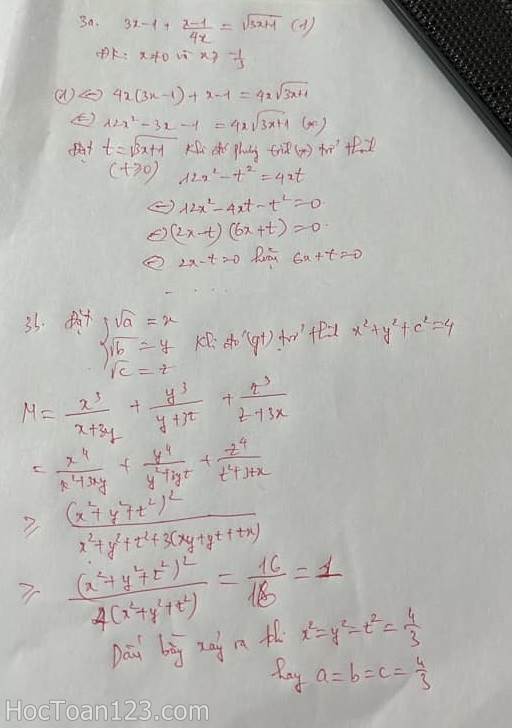
Câu 1c giải sai rồi tề :)))