KIẾN THỨC CẦN NHỚ
– Đặt tính với các chữ số cùng một hàng thì viết thẳng cột với nhau – Thực hiện phép toán theo thứ tự từ phải sang trái, hàng nào không trừ được thì ta mượn một đơn vị ở hàng bên cạnh.
CÁC DẠNG TOÁN
Dạng 1: Tính, đặt tính rồi tính
Phương pháp chung:
Bước 1: Đặt các chữ số cùng một hàng thẳng cột với nhau
Bước 2: Thực hiện tính từ phải sang trái
– Các hàng có số bị trừ bé hơn số trừ thì ta mượn 1 đơn vị của hàng bên cạnh để thực hiện được phép trừ.
– Sau đó ta cộng lại 1 đơn vị vào số trừ của hàng vừa mượn, rồi tiếp tục thực hiện phép trừ như bình thường.
Dạng 2: Toán đố
Phương pháp chung:
Bước 1: Đọc và tìm hiểu đề bài
Đọc và ghi nhớ các dữ liệu đề bài đã cho, yêu cầu của bài toán.
Bước 2: Phân tích đề
Dựa vào câu hỏi của đề bài, chú ý các từ khóa “tất cả” hay “còn lại”, xác định phép toán cần sử dụng để tìm lời giải
Bước 3: Trình bày lời giải và kiểm tra lại đáp án
Dạng 3: Tìm x
Phương pháp chung:
Ghi nhớ lại cách giải khi tìm số hạng hoặc số bị trừ/số trừ còn thiếu.
+ Tìm số hạng còn thiếu: Lấy tổng trừ đi số hạng còn thiếu.
+ Tìm số bị trừ còn thiếu: Lấy hiệu cộng với số trừ
+ Tìm số trừ còn thiếu: Lấy số bị trừ trừ đi hiệu
BÀI TẬP VÍ DỤ
Ví dụ 1: Đặt tính rồi tính: 435 – 227
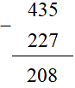
Bài giải:
- 5 không trừ được cho 7, lấy 15 trừ 7 bằng 8, viết 8
- 2 cộng 1 bằng 3, 3 trừ 3 bằng 0, viết 0
- 4 trừ 2 bằng 2, viết 2
Vậy 435 – 227 = 208
Ví dụ 2: Khối 2 và khối 3 của một trường A có 244 học sinh, trong đó khối 2 có 162 học sinh. Hỏi khối 3 có bao nhiêu học sinh?
Bài giải:
Số học sinh của khối 3 là:
244 – 162 = 82 (học sinh)
Đáp số: 82 học sinh
Ví dụ 3: Tìm x biết, 543 – x = 272.
Bài giải:
543 – x = 272
x = 543 – 272
x = 271
Vậy x = 271.

